Yangsanity's Blog

搞懂 Trie

发表于 2020-10-28 分类于 data structure 阅读次数： Disqus：

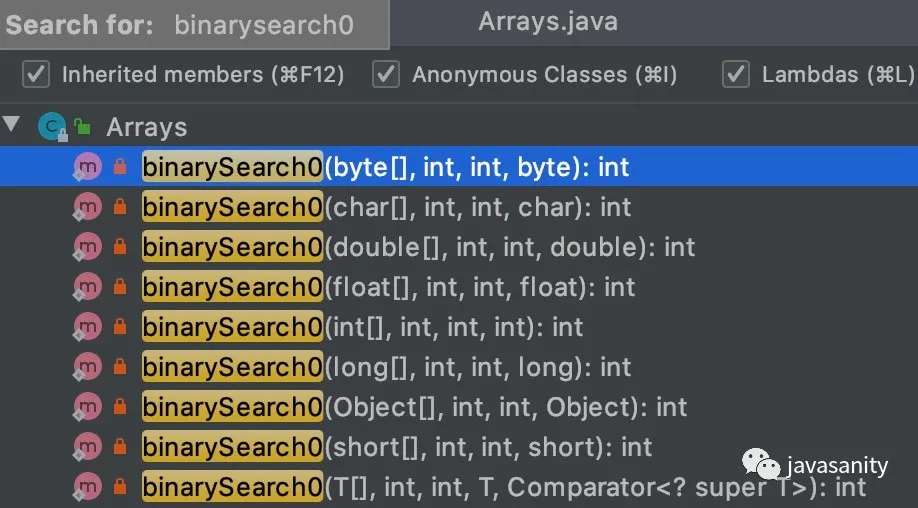
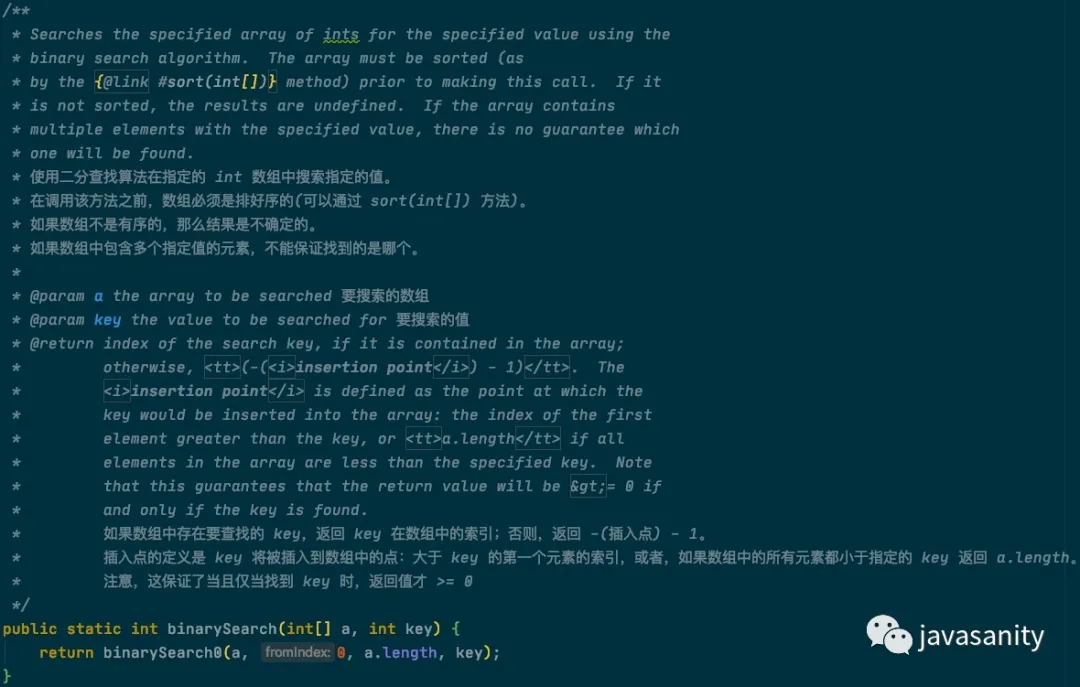
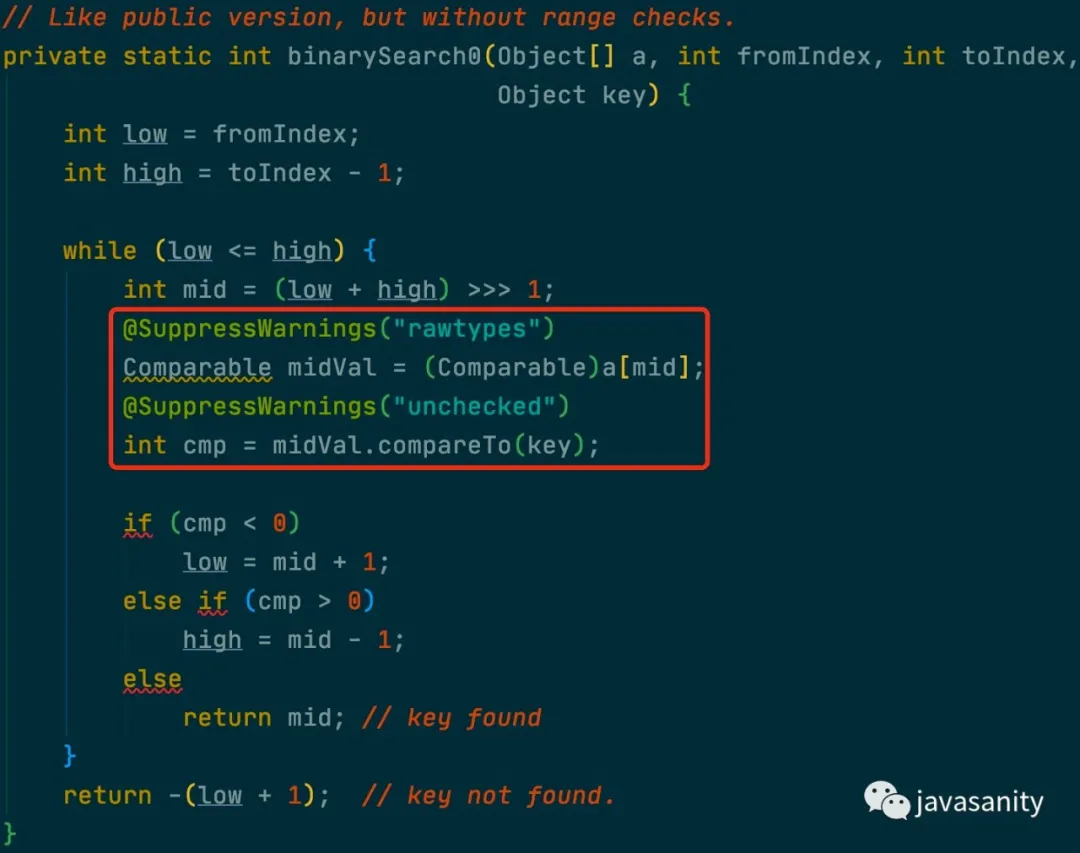
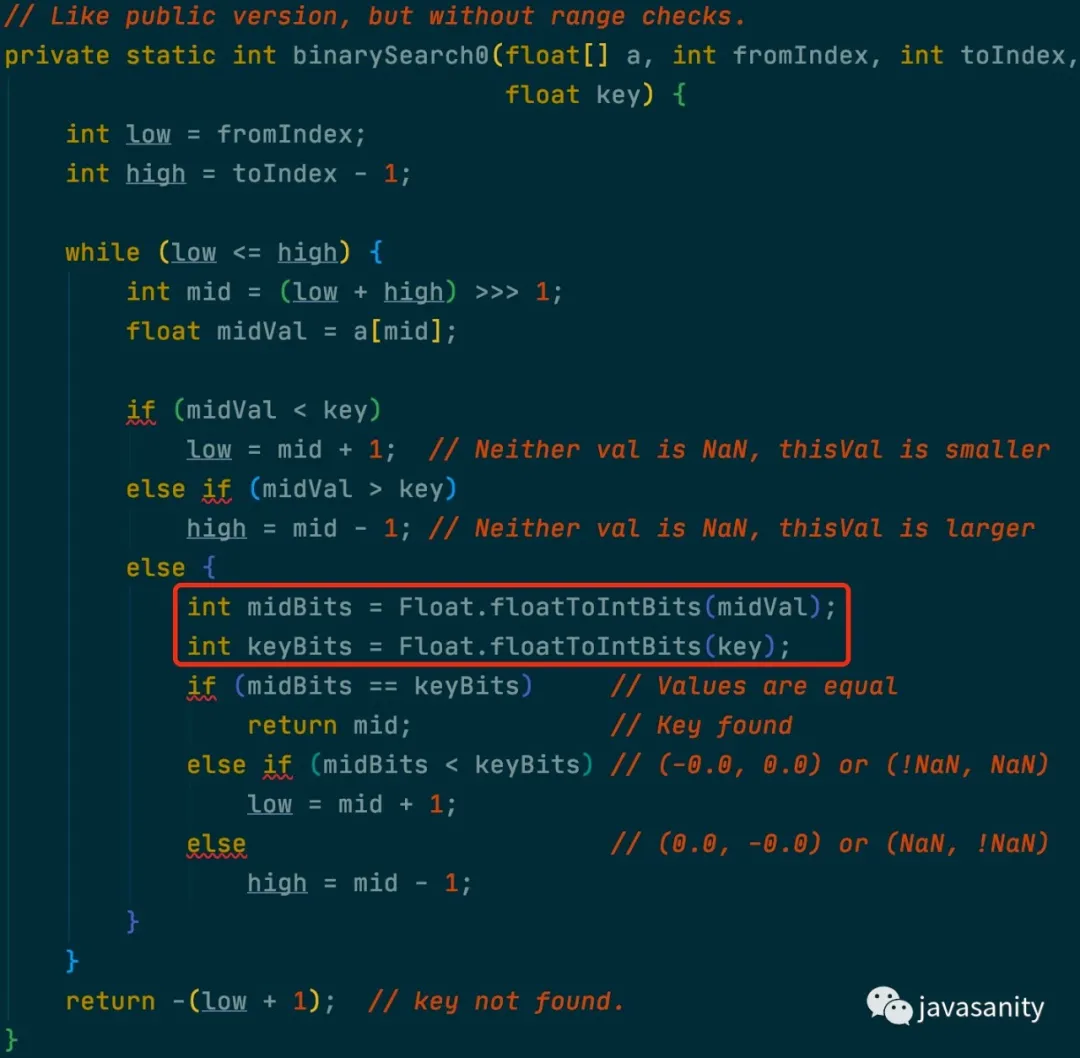
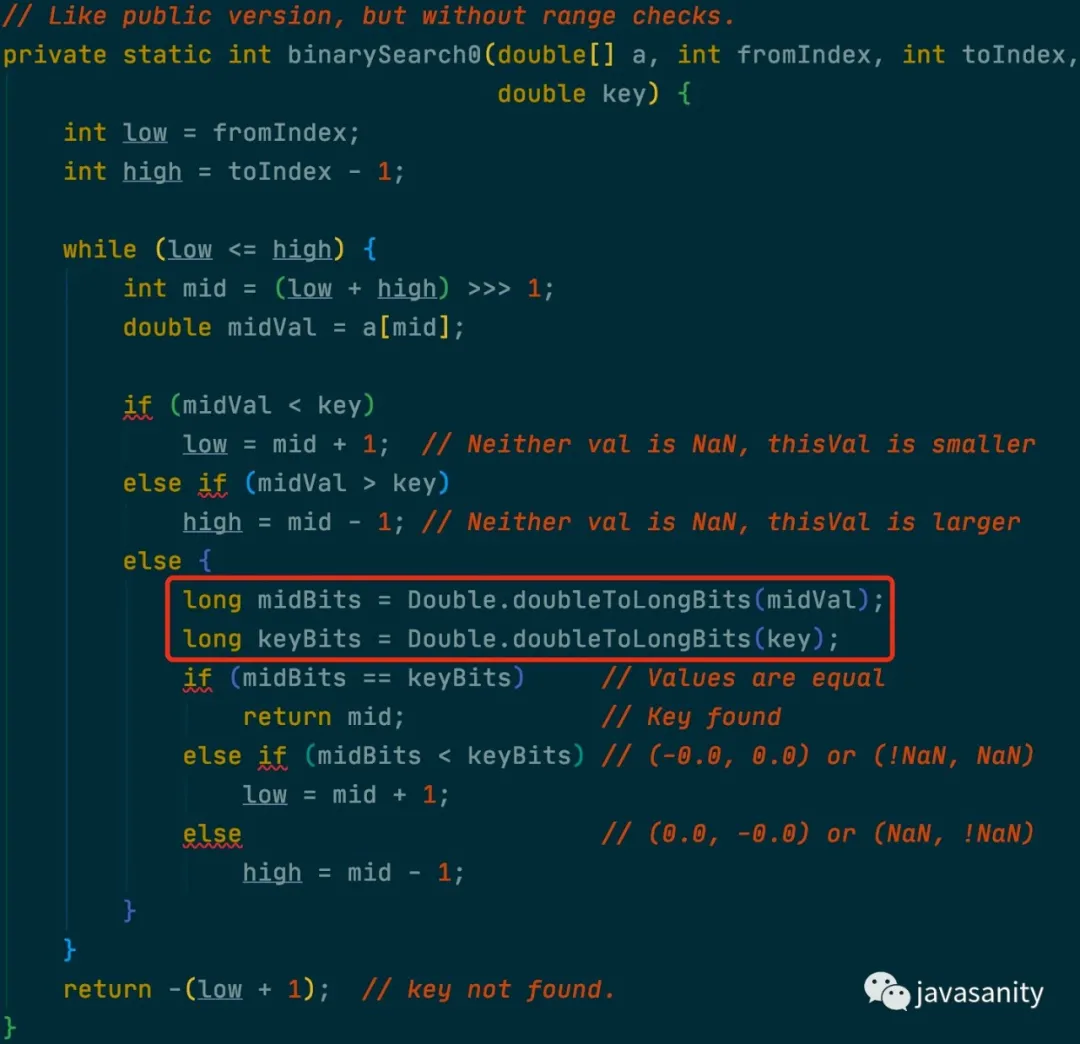
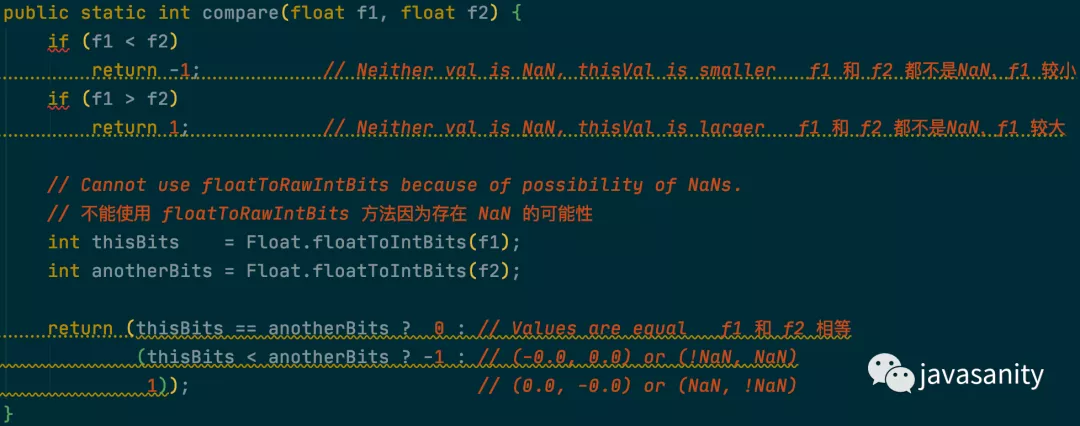
1

在计算机科学中，Trie 又称字典树或前缀树，顾名思义，它是一个树形结构。Trie 树通常专门用来处理字符串，解决在一组字符串集合中快速查找某个字符串的问题。

Trie 的典型应用就是自动补全、搜索提示等。例如命令行或 ide 的自动补全；例如在搜索引擎中输入一个关键字或网址，可以自动弹出可能的选择，而当没有完全匹配的搜索结果时，可以返回前缀最相似的可能结果。

利用 Trie 树可以做到：查询每个字符串的时间复杂度和字符串总数量无关，只和查询字符串的长度有关。

怎么做到的呢？

在实现上，Trie 是一棵多叉树。存储时，将每个字符串以字符为单位拆开存储在每个节点上，利用字符串之间的公共前缀，将重复的前缀合并在一起。结构如下图：

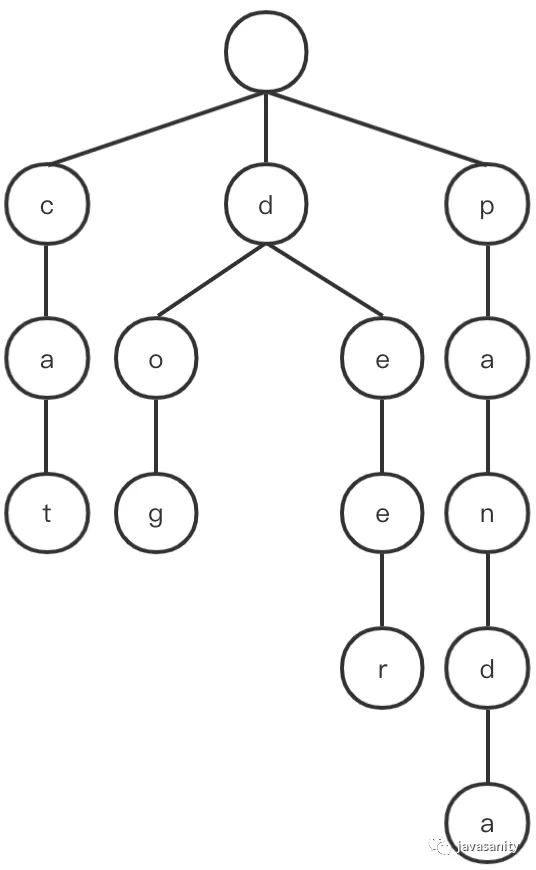
可以看到，在这棵树上，每个节点的所有子孙节点都有相同的前缀，而根节点是一个空节点，不包含任何信息。

这样，查找任何字符串，从根节点出发，最多需要查询字符串的长度即可找到相应的字符串。

定义节点

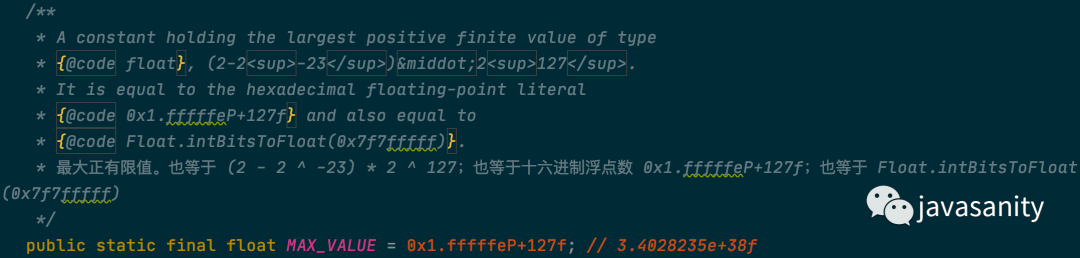
我们知道，英文字母表中一共有 26 个英文字母，所以相应地每个节点应该有 26 个指针指向下一个节点，所以在 Trie 中每个节点可以这样定义：

class Node {

    /**
     * 字符
     */
    char c;

    /**
     * 指向后续节点的指针
     * 初试时指定大小为 26
     */
    Node[] next;   
}

但是，考虑到不同语言，不同情境，比如要存储的字符串要包含大小写，或包含数字，或要存储的字符串是网址，或邮件地址，甚至更加复杂的内容时，26 个指针是不够的。当然某些情况下，26 个指针又太富裕，会造成不必要的浪费。

这样看来，直接写死 26 并不太好，至少不够灵活，除非我们能非常确定我们的业务场景只需要有固定的 26 个指针。我们希望最好能够用动态的方式来解决这个问题，怎么做呢？我们可以用 Map<char, Node> 来作为 next 的实现。

class Node {

    /**
     * 字符
     */
    char c;

    /**
     * 指向后续节点的指针
     */
    Map<Character, Node> next;   
}

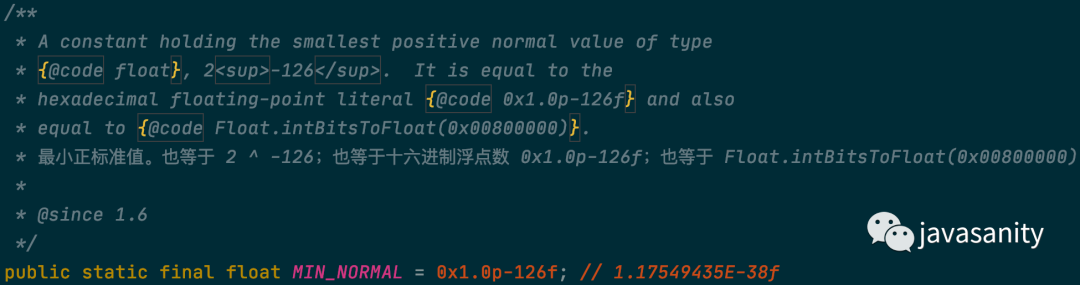
再仔细想想，当我们要在 Trie 中搜索某个字符串时，其实已经知道接下来要搜索的字符是什么了。所以更准确来讲，我们应该把字符标到 Trie 的边上，如下图：

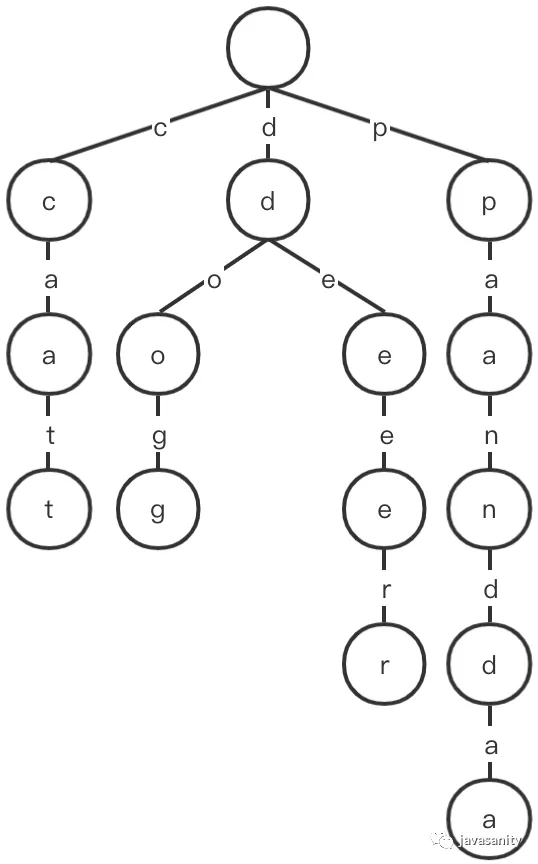
因此，在 Node 节点的实现中其实并不用保存这个字符的值。（当然，也得承认，某些情况下在节点中多存储一些信息可以帮助我们更快的组织某些逻辑）

class Node {

    /**
     * 指向后续节点的指针
     */
    Map<Character, Node> next;   
}

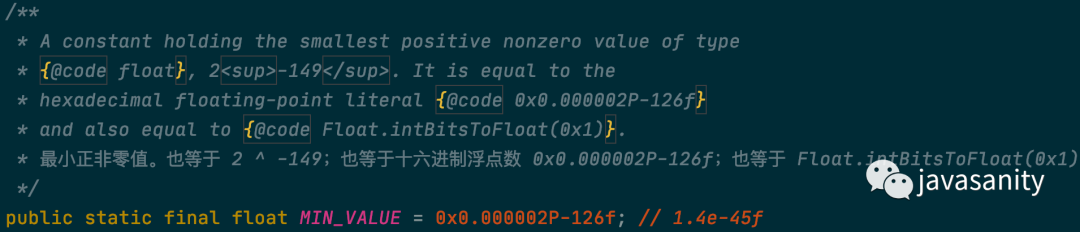
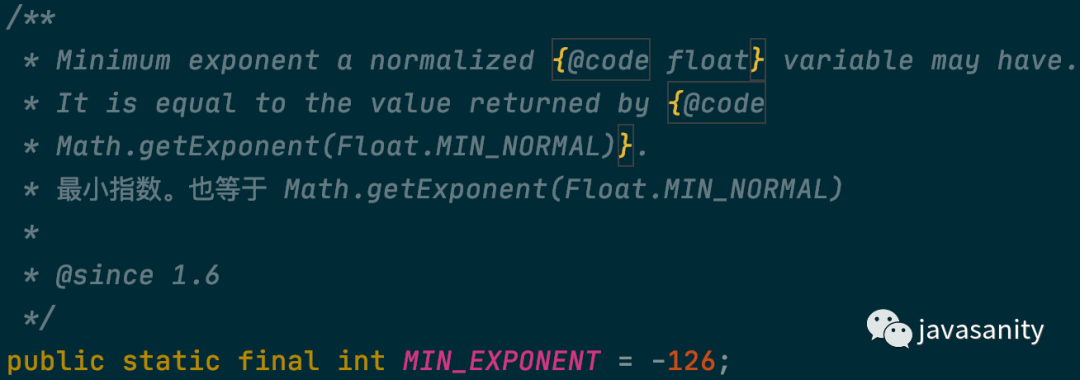
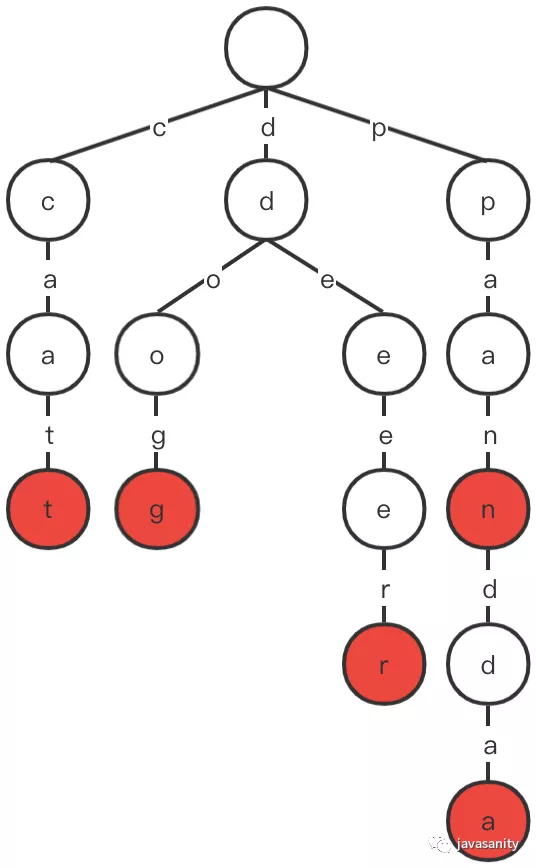
另外还有一个问题，就是有可能某个字符串是另一个字符串的前缀，这样我们就还需要知道哪些节点代表着这个字符串的结束。所以在每个 Node 中还需要再存储一个值来表示当前节点是否是某个字符串的结尾。

综上，最终的节点可以定义如下：

class Node {

    /**
     * 该节点是否是字符串的结尾
     */
    boolean isEndingChar;
    
    /**
     * 指向后续节点的指针
     */
    Map<Character, Node> next;   
}

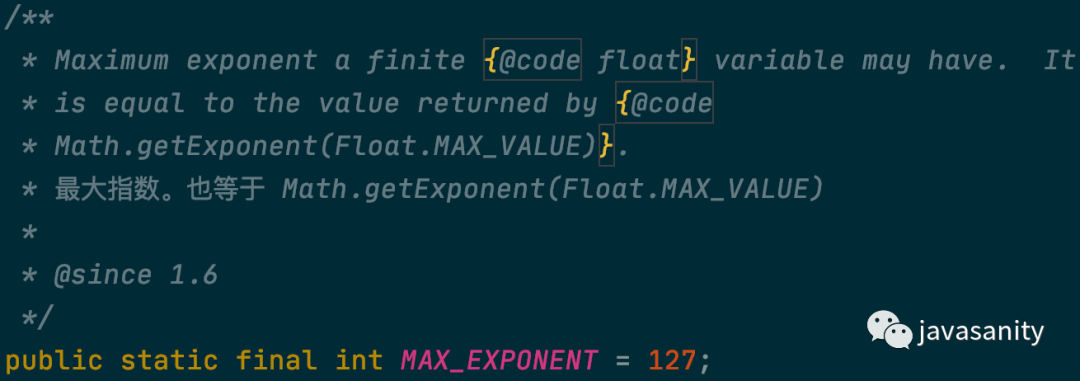
结构图如下（用红色节点来表示 isEndingChar 为 true）：

Trie 实现

Trie 树主要有三个操作：

将一个字符串插入到 Trie 树中
查询一个字符串是否在 Trie 树中
查询一个字符串在 Trie 树中是否作为某些字符串的前缀

接下来就可以动手来实现 Trie 了，这里给出两版实现。

用数组来实现

/**
 * 数组实现
 */
public class Trie {

    /**
     * The root node.
     */
    private final Node root;

    /**
     * Initialize the data structure.
     */
    public Trie() {
        root = new Node();
    }

    /**
     * Inserts a word into the trie.
     */
    public void insert(String word) {
        Node cur = root;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            int index = c - 'a';
            if (cur.next[index] == null) {
                cur.next[index] = new Node();
            }
            cur = cur.next[index];
        }
        cur.isEndingChar = true;
    }

    /**
     * search a prefix or whole key in trie and returns the node where search ends
     */
    private Node searchPrefix(String word) {
        Node cur = root;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            int index = c - 'a';
            if (cur.next[index] == null) {
                return null;
            }
            cur = cur.next[index];
        }
        return cur;
    }

    /**
     * Returns if the word is in the trie.
     */
    public boolean search(String word) {
        Node node = searchPrefix(word);
        return node != null && node.isEndingChar;
    }

    /**
     * Returns if there is any word in the trie that starts with the given prefix.
     */
    public boolean startsWith(String word) {
        Node node = searchPrefix(word);
        return node != null;
    }

    private static class Node {

        /**
         * 该节点是否是字符串的结尾
         */
        public boolean isEndingChar;

        /**
         * 指向后续节点的指针
         */
        public Node[] next;

        public Node(boolean isEndingChar) {
            this.isEndingChar = isEndingChar;
            next = new Node[26];
        }

        public Node() {
            this(false);
        }
    }
}

用 Map 来实现

import java.util.HashMap;
import java.util.Map;

/**
 * HashMap 实现
 */
public class Trie {

    /**
     * The root node.
     */
    private final Node root;

    /**
     * Initialize the data structure.
     */
    public Trie() {
        root = new Node();
    }

    /**
     * Inserts a word into the trie.
     */
    public void insert(String word) {
        Node cur = root;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            if (!cur.next.containsKey(c)) {
                cur.next.put(c, new Node());
            }
            cur = cur.next.get(c);
        }
        cur.isEndingChar = true;
    }

    /**
     * search a prefix or whole key in trie and returns the node where search ends
     */
    private Node searchPrefix(String word) {
        Node cur = root;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            if (!cur.next.containsKey(c)) {
                return null;
            }
            cur = cur.next.get(c);
        }
        return cur;
    }

    /**
     * Returns if the word is in the trie.
     */
    public boolean search(String word) {
        Node node = searchPrefix(word);
        return node != null && node.isEndingChar;
    }

    /**
     * Returns if there is any word in the trie that starts with the given prefix.
     */
    public boolean startsWith(String word) {
        Node node = searchPrefix(word);
        return node != null;
    }

    private static class Node {

        /**
         * 该节点是否是字符串的结尾
         */
        public boolean isEndingChar;

        /**
         * 指向后续节点的指针
         */
        public Map<Character, Node> next;

        public Node(boolean isEndingChar) {
            this.isEndingChar = isEndingChar;
            next = new HashMap<>();
        }

        public Node() {
            this(false);
        }
    }
}

虽然 Trie 树如此高效，但仍然有局限性，相信大家也发现了，那就是空间问题。在某些情况下，比如重复前缀并不多时，Trie 树甚至有可能会浪费更多的内存。

这个问题又该如何解决呢？

大的思路来说，就是要在查询效率和内存之间做平衡。所以，既然要省内存，我们就牺牲一点查询的效率。

这里介绍两种思路：

第一种思路叫做压缩字典树（Compressed Trie），即对只有一个子节点的节点，而且此节点不是一个字符串的结束节点，将此节点与子节点合并在一起。如下图所示：

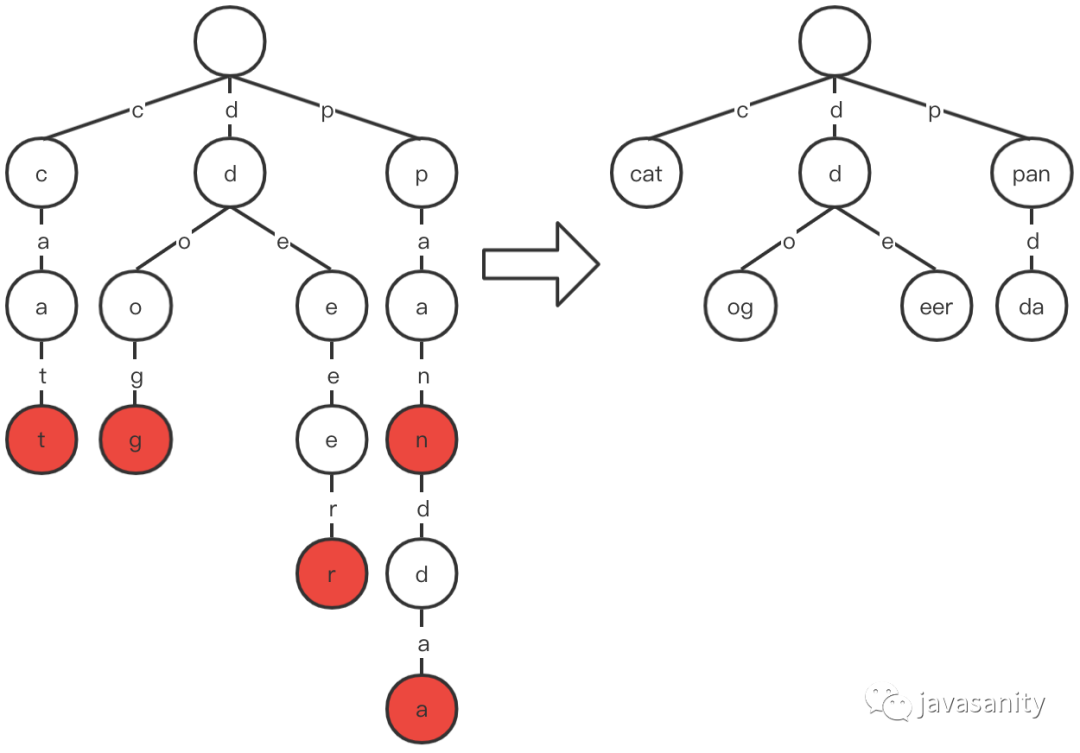
可以看到，空间明显减少，但是代价就是操作更复杂，维护成本更高，插入也会更费时。

第二种思路叫做三分搜索字典树（Ternary Search Trie），这种树每个节点只有三个孩子，对于任意一个节点，小于该节点字符的节点放到其左子树上，大于该节点字符的节点放到其右子树上，等于该节点字符的节点放到中间子树上。如下图所示一个三分搜索字典树的局部：

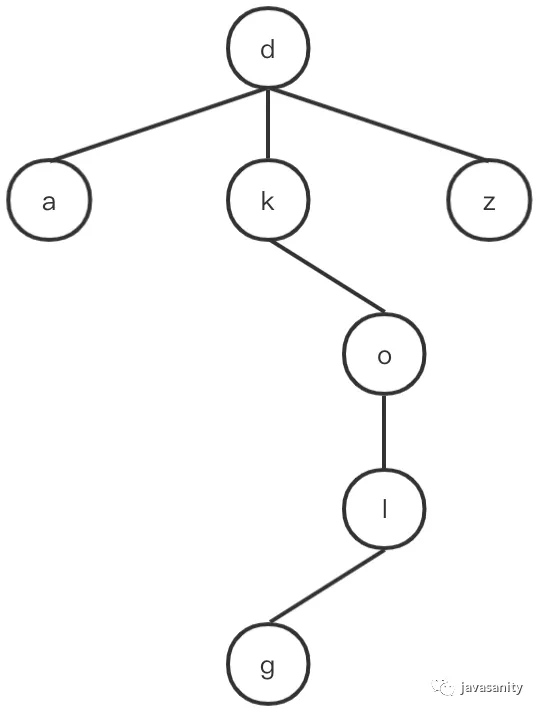
举个例子，我们要在上图中寻找 dog 这个字符串，第一个字符 d 等于 d，走中间的子树，第二个字符 o 大于 k，走右边的子树，第三个字符 g 小于 l，走左边的子树。

显然，这样时间复杂度会比字符串的长度要多，因为需要先判断当前要找的字符和当前节点字符的大小关系，再决定下一步往哪个方向走。

二分查找源码解析

发表于 2020-09-21 分类于 source code 阅读次数： Disqus：

之前一篇文章中已经解过一道 leetcode 二分查找的题目了，这篇文章再来分析一下 java 类库中提供的二分查找源码。

对应的类为 java.util.Arrays，方法名为 binarySearch。

1

可以看到：

贴心的提供了所有类型数组的二分查找方法
每种类型都提供了两种二分查找方法：
- 两个参数（最后一个三个参数）：从整个数组中查找
- 四个参数（倒数第二个五个参数）：从数组指定的范围中查找，中间的两个参数指定范围，该范围为前闭后开

每种类型数组的两种二分查找方法底层调用的都是同一个叫做 binarySearch0 的私有方法，因此 binarySearch0 也对应提供了不同类型的方法。binarySearch0 支持从数组指定的范围中查找，同样，中间的两个参数用来指定范围，该范围为前闭后开。

int[]

这部分主要以 int 类型数组的二分查找源码为例，来看看是怎么写的。

先来看两个参数的 binarySearch 方法。可以看到底层调用 binarySearch0 方法，中间两个参数是 0 和 a.length，即从数组 a 的 [0, a.length) 范围中查找目标值 key。

再来看四个参数的 binarySearch 方法。可以看到底层同样调用 binarySearch0 方法，中间两个参数是 fromIndex 和 toIndex，即从数组 a 的 [fromIndex, toIndex) 范围中查找目标值 key。

但是在调用 binarySearch0 方法之前，会调用 rangeCheck 方法来检查 fromIndex 和 toIndex 的合法性，不合法则抛出异常。

关于这两个参数的合法性，下面截图中方法注释的 @throws 部分写的非常明白（良心博主，翻译都安排的明明白白），不再赘述。

检查 fromIndex 和 toIndex 合法性的代码也非常简单。

最后来看 binarySearch0 方法，会发现，代码几乎和之前 leetcode 二分查找那篇文章中我们写的一样，唯一的区别是：如果没找到目标值 key 时的返回值。

关于这点，上面截图中方法注释的 @return 部分也写的非常明白，不再赘述。

关于没找到目标值 key 时为什么返回的是 -(插入点) - 1 的证明方法，在这里也共享出一个链接以供大家阅读：

https://blog.csdn.net/paralysed/article/details/106583034

3

其它类型数组的二分查找源码和 int 类型的大同小异，这部分来具体看看。

byte[]、char[]、long[]、short[] 和 int[] 一样，大小比较用的都是大于小于的方式
Object[] 大小比较用的是 Comparable.compareTo 方法

T[] 的大小比较，最后一个参数可以传自定义比较器，如果没传，则默认走的是 Object[] 的二分查找方法

float[] 和 double[] 的大小比较方法和前面类型的都有一点点不一样。不过还好，我们已经了解了 IEEE 754 标准，并且在上一篇一起分析过 Float.java 和 Double.java 的源码，所以，直接上代码（该部分代码对应其 compare 方法源码）

Float Double 部分源码解析

发表于 2020-09-16 分类于 source code 阅读次数： Disqus：

前几篇一直在说 IEEE 754 标准，搞明白了这个标准，再来看 java 中 Float.java 和 Double.java 的源码，很多变量和方法就能理解了。

1

Float 和 Double 都是继承了 Number 类并实现了 Comparable 接口。

Comparable 接口大家都熟悉，它只有一个 compareTo 方法，用来比较两个数值的大小。这个方法在 Float.java 和 Double.java 里都有实现，相关源码在下面会说到。

Number 类是个抽象类，里面一共 6 个方法，分别可以表示转换为基本类型 byte、 double、 float、 int、 long 和 short 的数值，但是转换的特定语义和转换细节是由子类实现来定义。

另外从 Number 类的类注释上也可以获得一个重要信息：转换可能会丢失关于数值总体大小的信息，可能会丢失精度，甚至可能返回与输入符号不同的结果。

Float 属性

这些属性都和前面介绍的 IEEE 754 标准有关，先回顾下第一篇文章中的总结：

形式	指数	小数部分
零	全为 0	全为 0
非规约形式	全为 0	大于 0 小于 1
规约形式	1 到 2ᵉ - 2（不全为 0 也不全为 1）	大于等于 1 小于 2
无穷	2ᵉ - 1（全为 1）	全为 0
NaN	2ᵉ - 1（全为 1）	非 0

正无穷

二进制表示为：0 11111111 00000000000000000000000

负无穷

二进制表示为：1 11111111 00000000000000000000000

NaN

二进制表示为：0 11111111 10000000000000000000000

最大值

二进制表示为：0 11111110 11111111111111111111111

1 2	(1.11111111111111111111111)₂ * 2¹²⁷ = (2 - 2 ^ -23)₁₀ * 2¹²⁷

最小正标准值

二进制表示为：0 00000001 00000000000000000000000

其实就是第一篇介绍 IEEE 754 文章中提到的：大于 0 部分的规约形式浮点数的最小值。

最小值

二进制表示为：0 00000000 00000000000000000000001

1
2
3

0.00000000000000000000001 * 2⁻¹²⁶
= 1 * 2⁻⁽¹²⁶⁺²³⁾
= 2⁻¹⁴⁹

其实就是第一篇介绍 IEEE 754 文章中提到的：大于 0 部分的非规约形式浮点数的最小值。

注意：虽然变量名叫 MIN_VALUE，但其实是个大于 0 的数。

最大指数

最小指数

位数

字节数

Float 方法

Float.floatToRawIntBits

是个 native 方法。它的作用是：将 float 浮点数转换为其 IEEE 754 标准二进制形式对应的 int 值。因为 float 和 int 都是 32 位，所以每一个 float 总有对应的 int 值。

如果参数为正无穷，则结果为 0x7f800000；如果参数为负无穷，则结果为 0xff800000；如果参数为 NaN，结果是表示实际 NaN 值的整数。

1	public static native int floatToRawIntBits(float value);

举两个例子大家就明白了：

1.0f

对应的二进制为 0 01111111 00000000000000000000000

那么 Float.floatToIntBits(1.0f) 的结果为：

1 2	2²³ + 2²⁴ + 2²⁵ + 2²⁶ + 2²⁷ + 2²⁸ + 2²⁹ = 1065353216

-1.0f

对应的二进制为 1 01111111 00000000000000000000000

那么 Float.floatToIntBits(-1.0f) 的结果为：

1
2
3

2²³ + 2²⁴ + 2²⁵ + 2²⁶ + 2²⁷ + 2²⁸ + 2²⁹ + 2³¹
= 3212836864
= -1082130432

（不要忘了整数会溢出，所以最终结果为溢出后的值）

Float.floatToIntBits

和 Float.floatToRawIntBits 方法几乎一样，唯一的区别是：对 NaN 作了检测，如果结果为 NaN，直接返回 0x7fc00000（即 Float.NaN）。

如果参数为正无穷，则结果为 0x7f800000；如果参数为负无穷，则结果为 0xff800000；如果参数为 NaN，则结果为 0x7fc00000。

前面的文章中介绍过，NaN 的阶码都为 1，尾数不全为 0，所以在 IEEE 754 标准中，NaN 并不是一个固定的值，而是一个范围。在 Java 中将 NaN 定义为了一个属性，在上边属性部分已经介绍过，它是一个固定的值。当结果处于 NaN 的范围中，此时会返回 Float.NaN 对应的值 0x7fc00000。

这一点在源码中也有体现。先调用 floatToIntBits 方法获取对应的 int 值，接下来检测 NaN，如果是 NaN，给返回值赋值为 0x7fc00000。

看看代码中是如何检测 NaN 的：

FloatConsts.EXP_BIT_MASK 是一个常量 2139095040，其对应的二进制表示为 0 11111111 00000000000000000000000
FloatConsts.SIGNIF_BIT_MASK 也是一个常量 8388607，其对应的二进制表示为 0 00000000 11111111111111111111111
检测阶码：result & FloatConsts.EXP_BIT_MASK，如果 result 是 NaN，那么 result 的阶码都为 1，运算结果仍然为 FloatConsts.EXP_BIT_MASK
检测尾数：result & FloatConsts.SIGNIF_BIT_MASK，如果 result 是 NaN，那么 result 的尾数不全为 0，运算结果肯定不为 0
如果同时满足了这两个条件，那么 result 就是 NaN，给返回值赋值为 0x7fc00000

& 运算：1 & 1 = 1；0 & 1 = 0；1 & 0 = 0

Float.intBitsToFloat

是个 native 方法。它的作用是：返回与给定参数表示相对应的浮点值。可以这么理解，和 floatToIntBits 做的事情刚好相反（其实从方法名也能看出来）。

如果参数为 0x7f800000，则结果为正无穷；如果参数为 0xff800000，则结果为负无穷；如果参数值在 0x7f800001 到 0x7fffffff 或在 0xff800001 到 0xffffffff 之间，则结果为 NaN。

1	public static native float intBitsToFloat(int bits);

从它的方法注释上还能得到一些有用的信息，比如：

Java 提供的任何 IEEE 754 浮点操作都不能区分具有不同位模式的两个同类型 NaN 值，不同的 NaN 值只能使用 Float.floatToRawIntBits 方法区分
根据参数如何求 s（符号位） e（阶码） m（尾数）：

1
2
3

int s = ((bits >> 31) == 0) ? 1 : -1;
int e = ((bits >> 23) & 0xff);
int m = (e == 0) ? (bits & 0x7fffff) << 1 : (bits & 0x7fffff) | 0x800000;

Float.compareTo

该方法直接调用了 Float.compare 方法，所以我们直接来看 compare 方法。

图中注释已经写的非常明白了，可以看到，两个浮点数的比较并不是想象中那么简单的，有一些特殊情况需要考虑。

Float.equals

Float.hashCode

重点是最后调用了 floatToIntBits 方法。

Float.isNaN

该方法直接调用了 isNaN(value) 方法，所以我们直接来看 isNaN(value) 方法，这个方法的判断逻辑也特别有意思。

可以看出，如果 v 为 NaN，则 v != v；如果 v 不为 NaN，则 v == v。

Double

同 Float，举一反三之。

浮点数的运算

发表于 2020-09-13 分类于 computer 阅读次数： Disqus：

这篇文章来看看浮点数是怎么进行四则运算的。

加减思路

首先来看两个十进制的小数如何进行相加和相减：

(1.6 * 10⁻⁵) + (0.3 * 10⁻⁶)
= (1.6 * 10⁻⁵) + (0.03 * 10⁻⁵)
= (1.6 + 0.03) * 10⁻⁵
= 1.63 * 10⁻⁵

(1.6 * 10⁻⁵) - (0.3 * 10⁻⁶)
= (1.6 * 10⁻⁵) - (0.03 * 10⁻⁵)
= (1.6 - 0.03) * 10⁻⁵
= 1.57 * 10⁻⁵

可以看到，两个十进制小数的加法或减法，要先做这一步：

(1.6 * 10⁻⁵) + (0.3 * 10⁻⁶) 
= (1.6 * 10⁻⁵) + (0.03 * 10⁻⁵)
或
(1.6 * 10⁻⁵) - (0.3 * 10⁻⁶) 
= (1.6 * 10⁻⁵) - (0.03 * 10⁻⁵)

原因很简单：两个小数相加，首先得把这两个数的小数点位置对齐。这么做的目的就是为了对齐小数点。然后就可以将相同的指数值作为公因数提出来，尾数再进行加减运算。

类比十进制，对于 IEEE 754 标准表示的二进制浮点数的加减运算，我们首先也要对齐小数点。从前面的文章我们知道，二进制浮点数其实也是科学计数法表示，要对齐小数点就要让两个浮点数科学计数法表示中的指数值相同，即要让两个浮点数的二进制表示中的阶码相同。这一步叫做对阶。

关于对阶，有个原则：小阶对大阶。意思就是指数小的浮点数的阶码要调整成指数大的浮点数的阶码。

这是因为对于二进制表示的浮点数来说，指数每升高一位，尾数就要右移一位，即尾数低位移出；反之，指数每降低一位，尾数就要左移一位，即尾数高位移出。相比之下，显然采用小阶对大阶损失的精度会更小，结果更准确。

所以，对阶的具体方法就是：小阶码加上大阶码和小阶码的差值，使之与大阶码相等，同时将小阶码对应的浮点数的尾数右移相应位数，以保证该浮点数的值不变（虽然还是避免不了损失一点精度）。

对阶之后，接下来进行尾数加减运算。

如果尾数进行加减运算后的结果是非规格化形式，需要依照 IEEE754 标准通过左规或右规来进行规格化操作（简单说就是转为 1.xxx * 2ⁿ 的形式）。

再多啰嗦一句，左规：尾数左移，阶码减值；右规：尾数右移，阶码加值。而右规操作一般只需将尾数右移一位即可，因为这种情况出现只会是尾数的最高位运算时出现了进位。

如果尾数过长，需要进行舍入处理。

浮点运算在对阶或右规时，尾数需要右移，被右移出去的位会被丢掉，从而造成运算结果精度的损失。为了减少这种精度损失，可以将一定位数的移出位先保留起来，在规格化后用于进行舍入处理。

关于这舍入处理，IEEE 754 标准给出了五种舍入规则：

英文其实也不是很难，我用 Chrome 插件翻译了一下，中文有点不太准确，但是对照着应该也不耽误理解。。

对于二进制舍入，一般我们用 0 舍 1 入法（类似于十进制中的 4 舍 5 入法）即可，即溢出数的最高位为 0 则直接舍去，为 1 则前一位进 1。

（这跟上一篇文章中将 -36.35 转为单精度二进制的例子第四步是一样的，当时少说了这一嘴，直接给了结果）

最后就要对结果做溢出判断。浮点数的溢出是根据其运算结果后阶码的值是否产生溢出来判断的。

如果阶码的值超过了阶码所能表示的最大正数，则为上溢，进一步，若此时浮点数为正数，则为正上溢，记为 +∞，若浮点数为负数，则为负上溢，记为 -∞；如果阶码的值超过了阶码所能表示的最小负数，则为下溢，进一步，若此时浮点数为正数，则为正下溢，若浮点数为负数，则为负下溢。正下溢和负下溢都作为 0 处理。

至此，浮点数加减法的思路就说完了。

乘除思路

同样，先来看两个十进制的小数如何进行相乘和相除：

1
2
3

(1.2 * 10²) * (1.3 * 10³)
= (1.2 * 1.3) * 10²⁺³
= 1.56 * 10⁵

1
2
3

(1.2 * 10²) / (1.2 * 10³)
= (1.2 / 1.2) * 10²⁻³
= 1 * 10⁻¹

可以看到，相乘：尾数相乘，指数相加；相除：尾数相除，指数相减。

类比十进制，对于 IEEE 754 标准表示的二进制浮点数的乘除运算，也是类似的。

但是最终结果的阶码可不只是两个数阶码简单的直接相加或相减。

用单精度浮点数来举例子，假设 a 的阶码为 Ea，指数的实际值为 x，b 的阶码为 E𝖻，指数的实际值为 y。那么 Ea = x + 127，E𝖻 = y + 127。

a * b 需要 Ea + E𝖻，但是结果的阶码可不仅仅是 Ea + E𝖻，因为 Ea + E𝖻 = (x + 127) + (y + 127) = (x + y) + 254，看到问题了吧，所以最终结果的二进制阶码为 Ea + E𝖻 - 127。

a / b 需要 Ea - E𝖻，但是结果的阶码也不仅仅是 Ea - E𝖻，因为 Ea - E𝖻 = (x + 127) - (y + 127) = x - y，看到问题了吧，所以最终结果的二进制阶码为 Ea - E𝖻 + 127。

当然，最终结果的阶码也可以直接用 x 和 y 相加减后的结果加上 127 再转为二进制。

接下来，尾数运算，规格化，舍入处理，判断溢出都同上。

至此，浮点数乘除法的思路也说完了。

加法 example

例：计算 1.6 + 0.3

1 2	(1.6)₁₀ = (0 01111111 10011001100110011001101)₂ (0.3)₁₀ = (0 01111101 00110011001100110011010)₂

对阶

0.3 的阶码小，所以 0.3 的阶码调整为 01111111，对应尾数调整为：0.01001100110011001100110 10（最后的 10 先保留起来）

尾数运算

规格化，本例无需规格化
舍入处理

1.11100110011001100110011‬ 10 舍入处理后为 1.11100110011001100110100

所以最终尾数为：11100110011001100110100

溢出判断

没有溢出，所以最终结果为：(0 01111111 11100110011001100110100)₂

减法 example

1 2	(1.6)₁₀ = (0 01111111 10011001100110011001101)₂ (0.3)₁₀ = (0 01111101 00110011001100110011010)₂

例：计算 1.6 - 0.3

对阶，同上
尾数运算

规格化，本例无需规格化
舍入处理

1.01001100110011001100110 01 舍入处理后为 1.01001100110011001100110

所以最终尾数为：01001100110011001100110

溢出判断

没有溢出，所以最终结果为：(0 01111111 01001100110011001100110)₂

乘法 example

例：*计算 1.5 * 0.3*

1 2	(1.5)₁₀ = (0 01111111 10000000000000000000000)₂ (0.3)₁₀ = (0 01111101 00110011001100110011010)₂

计算结果阶码

尾数运算

1 2	1.1 * 1.00110011001100110011010 = 1.110011001100110011001110

规格化，本例无需规格化
舍入处理

1.11001100110011001100111 0 舍入处理后为 1.11001100110011001100111

所以最终尾数为：11001100110011001100111

溢出判断

没有溢出，所以最终结果为：(0 01111101 11001100110011001100111)₂

除法 example

例：计算 1.5 / 0.3

1 2	(1.5)₁₀ = (0 01111111 10000000000000000000000)₂ (0.3)₁₀ = (0 01111101 00110011001100110011010)₂

计算结果阶码

尾数运算

1 2	1.1 / 1.00110011001100110011001 1001... = 1.01

规格化，本例无需规格化
舍入处理，本例也无需舍入

所以最终尾数为：01000000000000000000000

溢出判断

没有溢出，所以最终结果为：(0 10000001 01000000000000000000000)₂

IEEE 754 example

发表于 2020-08-26 分类于 computer 阅读次数： Disqus：

上篇文章（传送门）大家可能看得晕晕乎乎的，这篇就来举一些例子来帮助大家更直观的理解 IEEE 754 标准。

本文的举例对象仍然是单精确度浮点数（32位）。

首先回顾一下上篇最后的总结：

形式	指数	小数部分
零	全为 0	全为 0
非规约形式	全为 0	大于 0 小于 1
规约形式	1 到 2ᵉ - 2（不全为 0 也不全为 1）	大于等于 1 小于 2
无穷	2ᵉ - 1（全为 1）	全为 0
NaN	2ᵉ - 1（全为 1）	非 0

non-number

先看那三个简单且很好理解的特殊值：

+0：0 00000000 00000000000000000000000
-0：1 00000000 00000000000000000000000
+infinity：0 11111111 00000000000000000000000
-infinity：1 11111111 00000000000000000000000
NaN：s 11111111 fraction

对于 NaN 来说，s 可 0 可 1，fraction 不全为 0 即可

normal number

规约形式的浮点数无疑是日常使用最多的。

例：将 -36.35 转为单精度二进制

整数部分转二进制

36₁₀ = (00100100)₂

小数部分转二进制

之前的文章说过小数怎么转二进制，再复习一下吧：

小数部分乘以 2，取结果的整数部分，直到小数部分为 0 或者位数已达到所要求的精度为止
- 0.35 x 2 = 0.7，整数部分为 0
- 0.7 x 2 = 1.4，整数部分为 1
- 0.4 x 2 = 0.8，整数部分为 0
- 0.8 x 2 = 1.6，整数部分为 1
- 0.6 x 2 = 1.2，整数部分为 1
- 0.2 x 2 = 0.4，整数部分为 0
- 0.4 x 2 = 0.8，从这里开始接下来无限循环 0 1 1 0 …

所以 0.35₁₀ = (01011001100110011000110…)₂

计算阶码

整数二进制.小数二进制 = 00100100.01011001100110011000110

移动小数点，使二进制变成 1.xxx * 2ⁿ 的形式：

1.0010001011001100110011000110 * 2⁵

指数的实际值是 5，单精度浮点数的固定偏移值为 127，所以指数域编码值为 5 + 127 = 132。

(132)₁₀ = (10000100)₂，所以阶码为 10000100

单精确度浮点数的尾数部分为 23 位，所以取 1.xxx 小数点后 23 位得到尾数部分为：

00100010110011001100110

负数符号位为 1，所以 -36.35 的单精度二进制表示为：

1 10000100 00100010110011001100110

例：将 `00111001001010111110100000000000` 转为小数

这是一个正数，是一个规约形式的浮点数，先分为三段

0 01110010 01010111110100000000000

计算指数的实际值

(01110010)₂ = 114₁₀，减去单精度浮点数的固定偏移值 127 得指数的实际值为 114 - 127 = -13

在尾数前加上隐藏的整数 1，然后转为 1.xxx * 2ⁿ 的形式：

1.01010111110100000000000 * 2⁻¹³

指数实际值为负数，所以整数部分为 0，小数部分二进制为：

0.000000000000101010111110100000000000

计算小数

1 2	1 * 2⁻¹³ + 1 * 2⁻¹⁵ + 1 * 2⁻¹⁷ + 1 * 2⁻¹⁹ + 1 * 2⁻²⁰ + 1 * 2⁻²¹ + 1 * 2⁻²² + 1 * 2⁻²³ + 1 * 2⁻²⁵ = 0.000163942575455

subnormal number

非规约形式的浮点数转换方法其实也很简单。因为非规约形式的浮点数整数部分为 0，所以非规约形式的浮点数转换就相当于上边的小数部分转二进制。

从上篇文章我们知道，非规约形式的浮点数指数实际值为 -126，即最终转为 0.xxx * 2⁻¹²⁶ 的形式，也就是说按照小数部分转二进制的方法，当出现第 127 个数时，这个数就作为尾数的第一个数，后边的依次补上，直到小数部分为 0 或者位数已达到所要求的精度为止。这个就不举例了。

同理，将非规约形式的浮点数转为小数将更简单。

例：将 `00000000001000000000000000000000` 转为小数

这是一个正数，是一个非规约形式的浮点数，先分为三段

0 00000000 01000000000000000000000

计算小数

1 2	2⁻¹²⁸ ≈ 2.938735877056 * 10⁻³⁹

怎么样，对于 IEEE 754 的理解是不是更深刻了些？

1