树状数组 | Yangsanity's Blog

树状数组，又称二元索引树（Binary Indexed Tree），又以其发明者命名为 Fenwick 树。最早由 Peter M. Fenwick 于 1994 年提出。

上篇文章最后已经把树状数组能干什么说的非常清楚了。再简单回顾下，树状数组是一种可以动态维护数组前缀和的数据结构，它的主要功能是：

单点更新 update(i, v)：把序列 i 位置的数加上一个值 v；
区间查询 query(i)：查询序列 [1⋯i] 区间的区间和，即 i 位置的前缀和

其中单点更新和区间查询的时间复杂度都是 O(logn)，n 为需要维护前缀和的数组的长度。

重点是，单点更新和区间查询的时间复杂度都是 O(logn) 它是怎么做到的？

树状数组的神秘面纱

先来看看它到底长什么样子。（我感觉长的跟跳表还有点像）

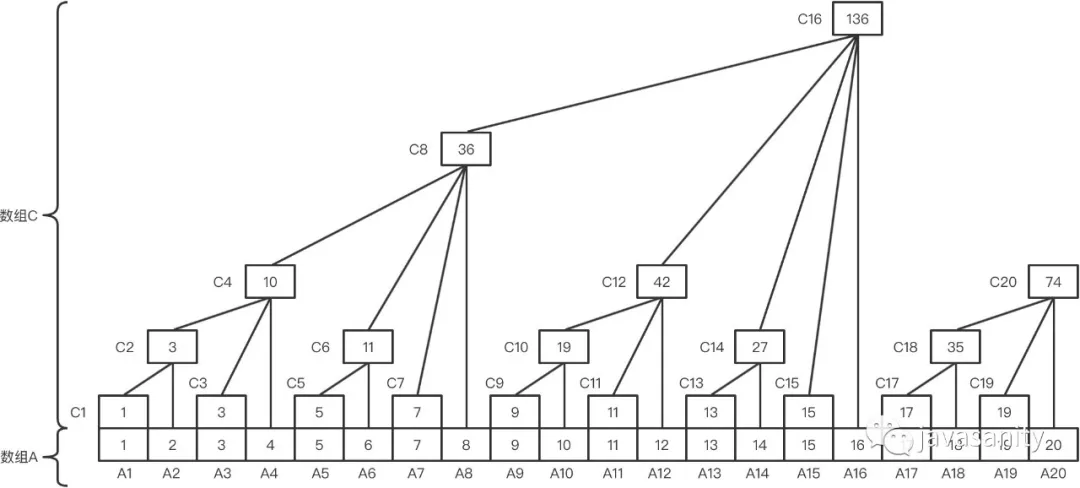
其中，数组 A 是原数组，数组 C 就是树状数组（现在终于知道它为什么叫树状数组了吧，长的就像树）。

从图中可以看到数组 A 和数组 C 之间的关系：

C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
… …

这里有个有趣的性质：设数组 C 的节点编号为 n，则 C[n] 管辖的区间为数组 A 从 n 往左连续 2 ^ k（k 为 n 二进制末尾 0 的个数）个元素。因为这个区间最后一个元素必然为 A[n]，所以 C[n] = Sum[ A[n – 2 ^ k + 1], A[n] ]。

好像有点绕，用 C[10] 来举个例子。10 的二进制表示为 1010，则 2 ^ k（k 为 10 二进制末尾 0 的个数，所以 k = 1）为 2 ^ 1 = 2，则 C[10] 管辖的区间为数组 A 从 10 往左连续 2 个元素，即 C[10] = Sum[ A[10 – 2 ^ 1 + 1], A[10] ] = A[9] + A[10]。

看到这里，大家应该就有感觉了，为什么树状数组能做到单点更新和区间查询的时间复杂度都是 O(logn) ？正是因为它把线性结构转化成了树状结构，从而进行跳跃式的扫描！

到这里，就得先说一个重要的函数 lowbit，它就是用来计算上面说的 2 ^ k 的快捷方法。

lowbit

lowbit(k) 的结果是：只保留 k 的二进制中最低位的 1。举个例子，lowbit(10)，10 的二进制是 1010，则 lowbit(10) = 0010（只保留 1010 中最低位的 1）。

而 lowbit 有两种实现方式，都要用到位运算。

实现方式一

我们知道，在计算机中，负数的二进制以原码的补码形式来表示，负数的补码为对该数的原码除符号位外各位取反，然后在最后一位加 1。

比如 -10 用二进制来表示：-10 的原码为 1000 0000 0000 0000 0000 0000 0000 1010；反码为 1111 1111 1111 1111 1111 1111 1111 0101；补码为 1111 1111 1111 1111 1111 1111 1111 0110。

此时，10 & -10 是什么情况呢？

0000 0000 0000 0000 0000 0000 0000 1010 & 1111 1111 1111 1111 1111 1111 1111 0110 = 0000 0000 0000 0000 0000 0000 0000 0010。惊喜的发现，其实结果就是 lowbit(10)。

（附 & 运算规则：0 & 0 = 0；0 & 1 = 0；1 & 0 = 0；1 & 1 = 1）

1
2
3

public int lowbit(int k) {
  return k & (-k);
}

实现方式二

我们知道，将一个二进制数减一，得到的结果是：从最低位的 1 开始后面的部分都与之前相反。

比如 10 的二进制表示为 1010，那么 9 的二进制表示为 1001。

此时，10 ^ 9 是什么情况呢？很简单，1010 ^ 1001 = 0011。

此时，10 & (10 ^ 9) 又是什么情况呢？也很简单，1010 & 0011 = 0010。我们又惊喜的发现，其实结果就是 lowbit(10)。

（附 ^ 运算规则：0 ^ 0 = 0；0 ^ 1 = 1；1 ^ 0 = 1；1 ^ 1 = 0）

1
2
3

public int lowbit(int k) {
  return k & (k ^ (k - 1));
}

树状数组实现思路

有了 lowbit 函数，我们就可以把上图中的 A 数组和 C 数组联系起来了！

单点更新

在修改时也要对该节点的所有父节点进行修改。比如在上图中要修改 C[1]，那么 C[2]，C[4]，C[8]，C[16] 也要做修改。

那不看图的话怎么知道该节点的所有父节点呢？不难，1 + lowbit(1) = 2，2 + lowbit(2) = 4，4 + lowbit(4) = 8，8 + lowbit(8) = 16，（16 + lowbit(16) = 32 超出了数组大小自然不用考虑）。

区间查询

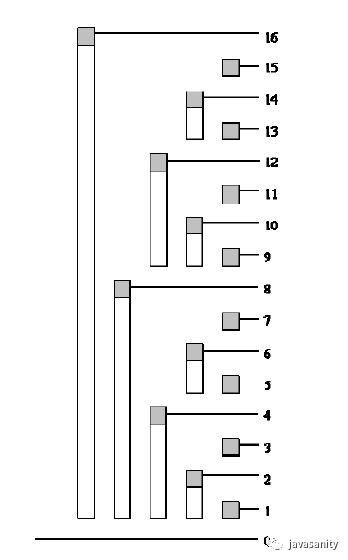
比如求上图中 [1, 14] 的区间和，从图中可以看到：
Sum[1, 14] = C[14] + C[12] + C[8] = Sum[ A[13], A[14] ] + Sum[ A[9], A[12] ] + Sum[ A[1], A[8] ] = Sum[ A[1], A[14] ]。

那不看图的话怎么算出 12 和 8 呢？也不难，14 - lowbit(14) = 12，12 - lowbit(12) = 8，（8 - lowbit(8) = 0 自然不用考虑）。

树状数组代码

/**
 * 树状数组
 */
public class FenwickTree {

    /**
     * 上图中的 C 数组
     */
    private int[] tree;

    private int len;

    public FenwickTree(int len) {
        this.tree = new int[len + 1];
        this.len = len;
    }

    /**
     * 单点更新：把数组 i 位置的值加上 v
     */
    public void update(int i, int v) {
        // 类比上图，从下到上进行更新
        while (i <= this.len) {
            this.tree[i] += v;
            i += lowbit(i);
        }
    }

    /**
     * 区间查询：查询序列 [1 ⋯ i] 区间的区间和，即 i 位置的前缀和
     */
    public int query(int i) {
        // 类比上图，从右到左查询
        int sum = 0;
        while (i > 0) {
            sum += this.tree[i];
            i -= lowbit(i);
        }
        return sum;
    }

    private int lowbit(int x) {
        return x & (-x);
    }
}

求数组中的逆序对

具体思路上篇文章最后已经介绍了，不再赘述，直接来看代码吧。

/**
 * 用离散化树状数组求求数组中的逆序对
 * 离散化原因：使得数字更紧凑，节约树状数组的空间
 */
public int reversePairs(int[] nums) {
    int len = nums.length;
    if (len < 2) {
        return 0;
    }
    // 去重并排序
    Set<Integer> treeSet = new TreeSet<>();
    for (int num : nums) {
        treeSet.add(num);
    }
    // 把排名存在 HashMap 里方便查询
    Map<Integer, Integer> rankMap = new HashMap<>();
    int rankIndex = 1;
    for (Integer num : treeSet) {
        rankMap.put(num, rankIndex++);
    }
    // 在树状数组内部完成前缀和的计算
    // 规则是：从后向前，先给对应的排名 + 1，再查询前缀和
    FenwickTree fenwickTree = new FenwickTree(rankMap.size());
    int count = 0;
    for (int i = len - 1; i >= 0; i--) {
        int rank = rankMap.get(nums[i]);
        fenwickTree.update(rank, 1);
        count += fenwickTree.query(rank - 1);
    }
    return count;
}

提交，完美通过！

凑字数

借用一句话来总结树状数组：树状数组巧妙地利用了二分，它并不神秘，关键是巧妙！