今天给大家带来一道 leetcode 的算法题。为什么这篇文章要写一道算法题?其实主要是想说之前写的排序算法可不只是为了面试用的。
这句话也算是一个小提示,那么你能不能与之前写的排序知识联系起来想到解法呢?
暴力
没啥好说的,一上来,两层 for 循环暴力枚举所有数对,逐一判断即可搞定。
1 | /** |
结果当然可想而知,毕竟时间复杂度为 O(n^2)。此外空间复杂度为 O(1)。
归并排序
利用归并排序的思路解这道题,你想到了吗?
前面写归并排序的时候写过归并排序的思路,希望你还有印象(没印象的话可以点击文章底部链接去看看哦)。
其实解这道题我们只需要在 merge 操作上做些思考。还记得 merge 操作吧,它是要把两个有序数组合并成一个有序数组。而我们思考的方向,既可以在左边的有序数组上,也可以在右边的有序数组上,所以这个思路可以有两种写法。下面逐一说明。
在左边的有序数组上思考
假定待 merge 数组如下,记逆序对总数为 ret: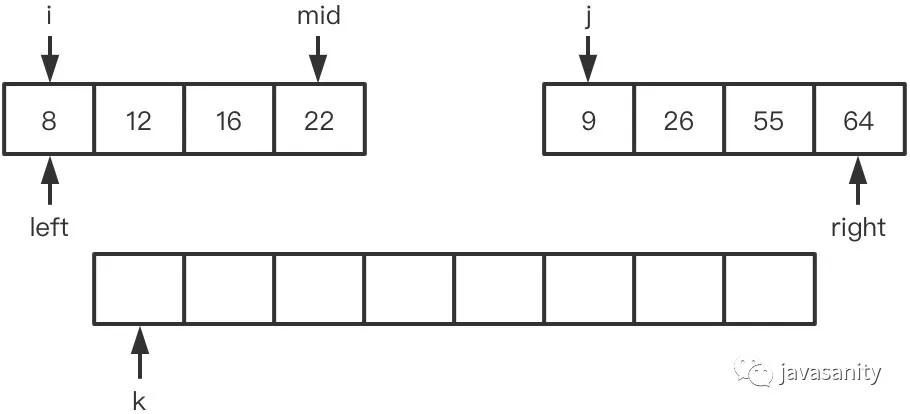
(1)8 < 9,不构成逆序对,此时 ret = 0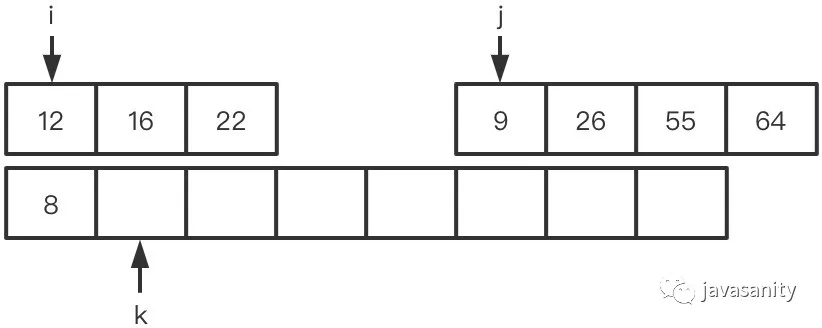
(2)12 > 9,构成逆序对,且左数组中 12 后边的数都和 9 构成逆序对,此时 ret = 3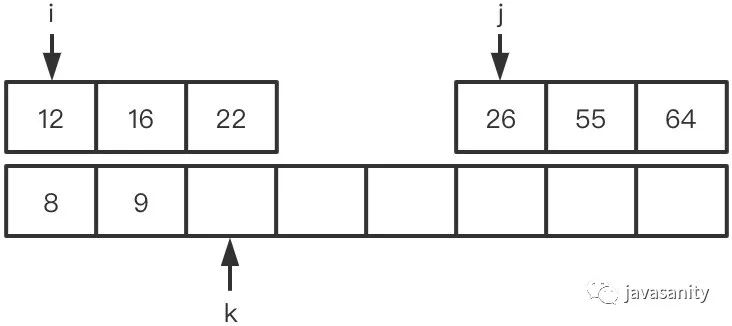
(3)12 < 26,不构成逆序对,此时 ret = 3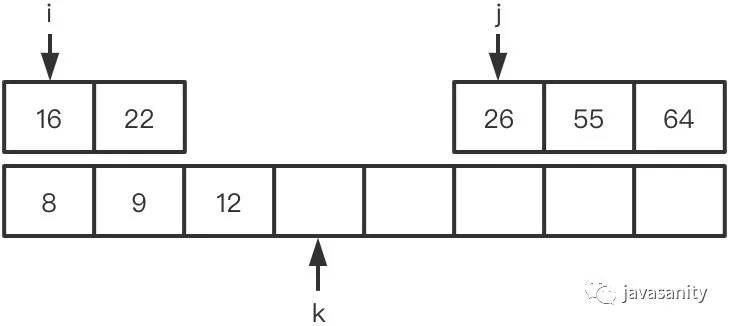
(4)16 < 26,不构成逆序对,此时 ret = 3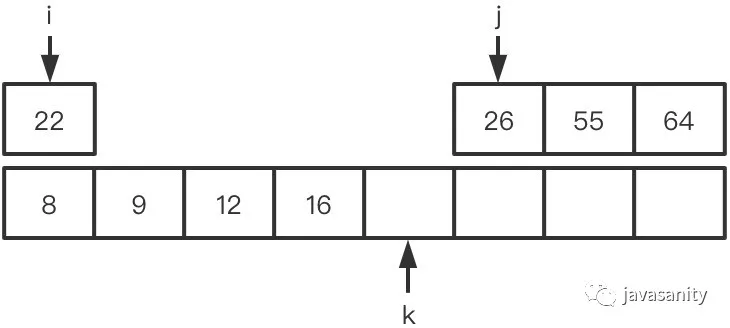
(5)22 < 26,不构成逆序对,此时 ret = 3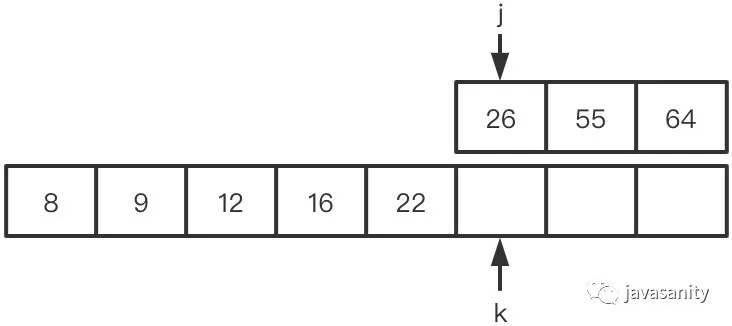
(6)左数组遍历完,右数组剩下的元素入辅助数组。因为此时右数组剩下的值比原左数组的所有值都大,不会构成逆序对,所以这一轮 merge 的最终 ret = 3
1 | /** |
在右边的有序数组上思考
要比在左数组思考多考虑一点点,不过也比较简单。
假定待 merge 数组如下,记逆序对总数为 ret: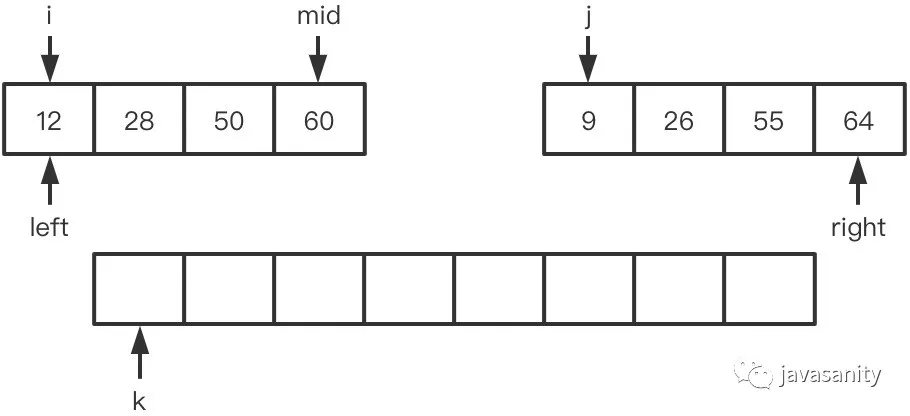
(1)12 > 9,ret 不变,此时 ret = 0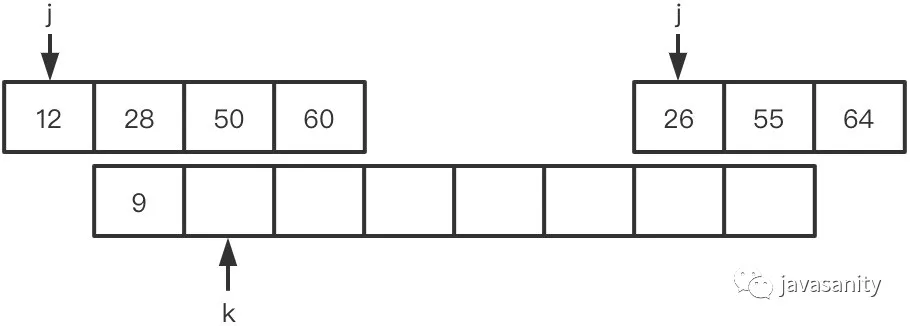
(2)12 < 26,12 和右数组 26 之前的所有数构成逆序对,此时 ret = 1
(3)28 > 26,ret 不变,此时 ret = 1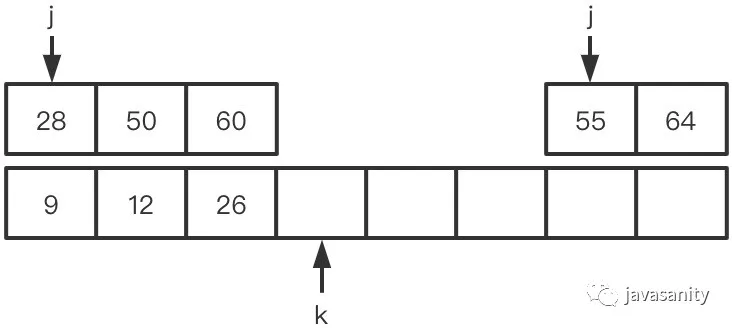
(4)28 < 55,28 和右数组 55 之前的所有数构成逆序对,此时 ret = 3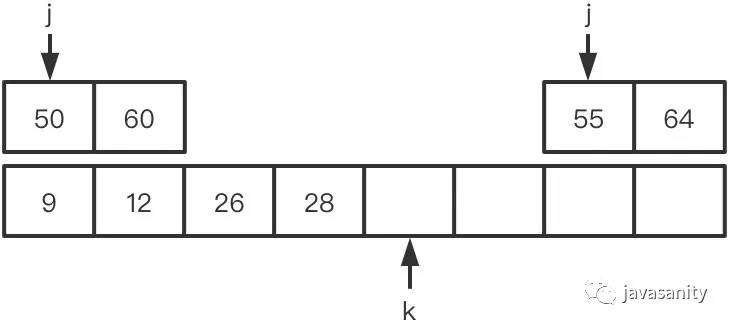
(5)50 < 55,50 和右数组 55 之前的所有数构成逆序对,此时 ret = 5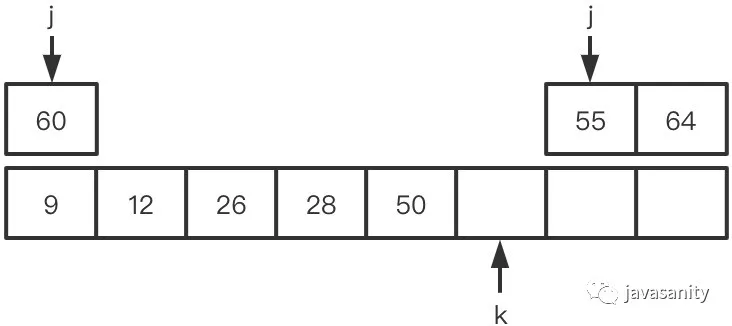
(6)60 > 55,ret 不变,此时 ret = 5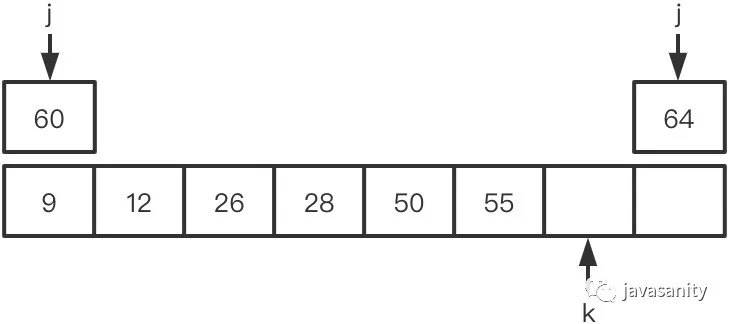
(7)60 < 64,60 和右数组 64 之前的所有数构成逆序对,此时 ret = 8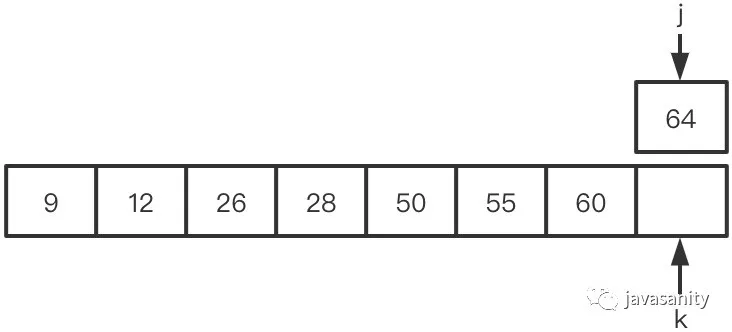
(8)左数组遍历完,右数组剩下的元素入辅助数组。因为此时右数组剩下的值比原左数组的所有值都大,不会构成逆序对,所以这一轮 merge 的最终 ret = 8
注意,为什么说要比在左数组思考多考虑一点,就在这里。如果最后的情况是右数组遍历完,左数组剩下的元素入辅助数组。那么此时左数组剩下的值比原右数组的所有值都大,那么此时左数组剩下的值都和原右数组的所有值都能构成逆序对,这部分一定要计算在内!
1 | /** |
提交成功通过。时间复杂度同归并排序 O(n * logn),空间复杂度也同归并排序 O(n)。
离散化树状数组
这个是从官方的解法中看到的,比较骚气,不过要用到一种新的数据结构 - 树状数组。
接下来说一下树状数组解这道题的思路吧,具体的树状数组和代码想放到下一篇再来写。
树状数组是一种可以动态维护数组前缀和的数据结构,它的主要功能是:
- 单点更新 update(i, v):把序列 i 位置的数加上一个值 v,在这道题中 v = 1
- 区间查询 query(i):查询序列 [1⋯i] 区间的区间和,即 i 位置的前缀和
其中单点更新和区间查询的时间复杂度都是 O(logn),n 为需要维护前缀和的数组的长度。还要注意,树状数组中 0 索引位置是不参与计算的。(具体原因了解树状数组后就能理解)
假定数组 a 为 [5, 5, 2, 3, 6],记逆序对总数为 ret。我们申请一个新数组,遍历 a,在新数组中记录 a 中每个值出现的次数,最终新数组结果如下:
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| value | 0 | 0 | 1 | 1 | 0 | 2 | 1 |
可以看到,a[i] 的前缀和可以表示:a 数组中有多少个数比 a[i] 小。那么,如果 a[i] 之前的数在原数组中是出现在 a[i] 后面的,那么 i - 1 的前缀和就代表这些数和 a[i] 构成的逆序对数量。
明白了这一点,那就好做了。我们可以从后往前遍历 a,当遍历到 a[i] 时,把对应的新数组中 i 位置的值自增 1,然后再计算 i - 1 的前缀和,记到 ret 中。当 a 遍历完成后,ret 即为逆序对总数。
为什么可以这么做呢?因为我们在遍历 a 的过程中,把 a 分成了两部分,一部分遍历过(在新数组中),另一部分待遍历(不在新数组中)。那么对于 a[i] 来说,我们求到的 i - 1 位置的前缀和,就是遍历过的元素中比 a[i] 小的元素的总和,而这些元素在 a 中本来就是排在 a[i] 后面的,但它们的值是比 a[i] 小的,所以这就形成了一个逆序对。
离散化树状数组
确实像上面说的那么做是可以的,但是别忘了题目的限制:0 <= 数组长度 <= 50000,额,其实这个限制还好,内存中放得下。如果限制更大一点,内存中放不下怎么办呢?
其实,就算限制更大一点,大到内存中都放不下,但是给定的数组中肯定也是很多位置是 0,它的有效元素的位置是稀疏的。我们可以想办法让有效位置紧凑一点,减少无效位置的出现,减少空间浪费,这时我们就可以用到这个方法 - 离散化。
也就是说,我们只需要关心有效元素在数组中按大小的排名,来决定它们在数组中的位置即可。
恰好,java 里有一种数据结构可以做到去重并排序这一点,什么呢?就是 TreeSet。
离散化树状数组解这道题的思路大致就说完了。其实有个非常重要的点没有说,那就是:单点更新和区间查询的时间复杂度都是 O(logn) 这个是怎么做到的?如果明白了这一点,那么他为什么叫“树状数组”也就明白了。好了,写不少字了,卖个关子吧。