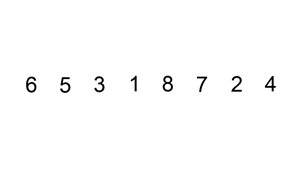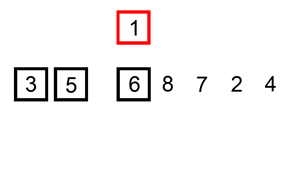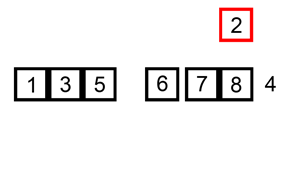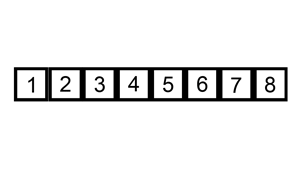Yangsanity's Blog

归并排序

发表于 2020-04-23 分类于 algorithm 阅读次数： Disqus：

归并排序（merge sort）是1945年由科学家约翰·冯·诺伊曼（John von Neumann）首次提出的，它是分治法的一个非常典型的应用。

当然，它也是面试中算法的一个高频考察点。（一说到面试，你是不是都有动力看下去了呢）

归并排序思想

首先简单介绍一下分治法（Divide and Conquer）。在计算机科学中，分治法是基于多项分支递归的一种很重要的算法范式。在每一层递归上一般有三个步骤：分解，解决，合并。分治的字面意思是“分而治之”，就是把一个复杂的问题分成多个相同或相似的子问题，最终子问题可以简单的直接求解，然后合并子问题的解即可得到原问题的解。这个思想也是很多高效算法的基础。

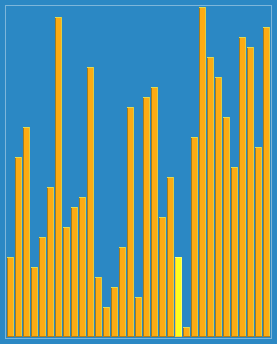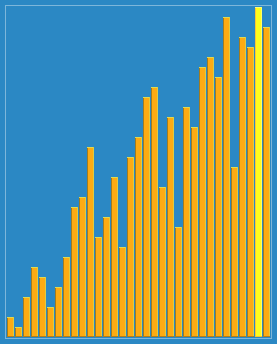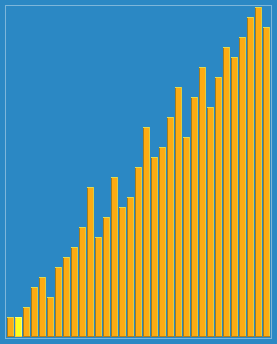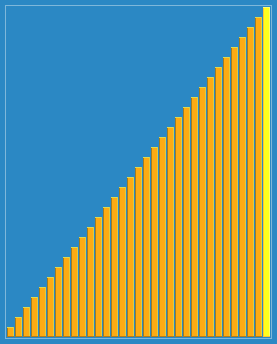
接下来就演示一下归并排序的整个过程吧。这次就不用文字来描述了，直接用两张图，因为图更直观些，相信看完你就能明白。

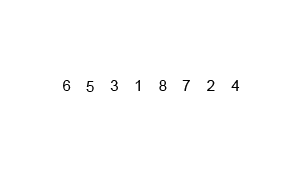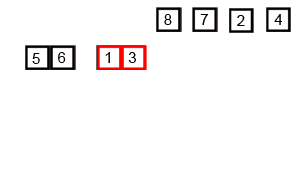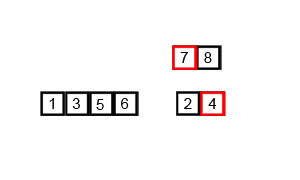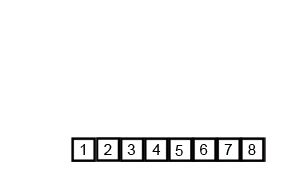
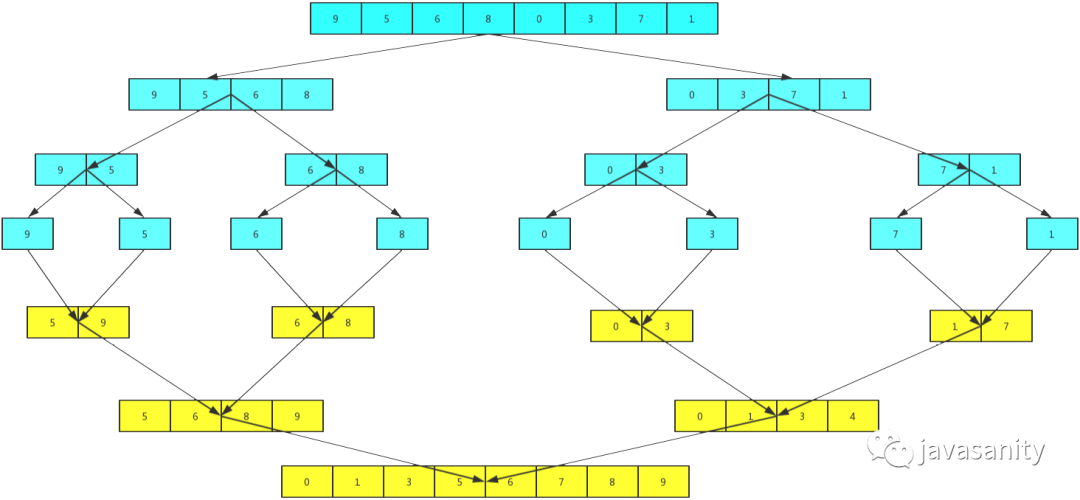
从demo中，我们可以看到，归并排序算法整体上可以分为两个部分：

分组：递归地把当前数组分割成两部分，直到不可再分割为止，此时，每个数组中只有一个元素；
归并（merge）：将两个已经有序的数组合并成一个有序的数组，最终，就会得到一个排好序的数组。

可以看到 merge 操作的代码写的怎么样基本上就决定了归并算法的好坏，那么应该怎么写呢？大家可以先思考一下。

这个问题是一个典型的“看起来比较简单，真正操作起来会发现其实并没有那么简单”的问题。merge 的过程通常不能直接在原数组上通过交换位置来完成，而是需要开辟一个同样大小的临时空间来辅助完成这个过程。

当使用这个临时空间后，归并的过程就变得比较容易。但这也算是归并排序的一个缺点，即多使用了O(n)的存储空间。不过在现代的计算机中，时间效率要比空间效率重要的多。因为无论是内存也好，或者硬盘也好，都变得越来越廉价，可以存储的数据规模也越来越大，因此，如果数据存储空间不是算法过程中的瓶颈，我们设计的算法通常优先考虑时间复杂度。

归并排序代码

在 merge 的代码实现上，主要思路是用三个索引来在数组内进行追踪。如下图：

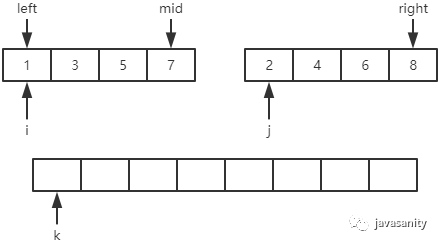
其实定义上图中的这些变量非常重要，举个例子，假如上图中定义的 mid 指向的是 2，那么写出来的代码就是完全不一样的。

在真正写代码之前，还要再啰嗦一句。其实归并排序的代码可以有两种写法：“Top-down”和“Bottom-up”，或者也可以称为“自顶向下”和“自底向上”，或者也可以称为“递归法”和“非递归法”（迭代法）。不要慌，下面都会给出代码示例。

/**
 * mergeSort：Top-down；自顶向下；递归法
 * @param data 待排序数组
 */
public void mergeSort(int[] data){
  sort(data, 0, data.length - 1);
}

/**
 * sort
 * @param data 待排序数组
 * @param left 起始index
 * @param right 结尾index
 */
private void sort(int[] data, int left, int right) {
  if (left >= right) {
    return;
  }
  int mid = left + ((right - left) >> 1);
  sort(data, left, mid);
  sort(data, mid + 1, right);
  // 对 data[left...mid] 和 data[mid + 1...right] 两部分进行归并，merge 方法代码见下
  merge(data, left, mid, right);
}

/**
 * mergeSort：Bottom-up；自底向上；非递归；迭代法
 * @param data 待排序数组
 */
public void mergeSort(int[] data){
  int n = data.length;
  // 第一层循环对 merge 的元素个数进行遍历，结果为（1，2，4，8，16，...）
  // 第二层循环中 j 为每一轮要进行归并的两个有序数组中左边数组的起始位置
  for (int i = 1; i < n; i *= 2) {
    for (int j = 0; j < n - i; j += 2 * i) {
      // 对 data[j...j + i - 1] 和 data[j + i...j + 2 * i - 1] 两部分进行归并，merge 方法代码见下
      merge(data, j, j + i - 1, Math.min(j + 2 * i - 1, n - 1));
    }
  }
}

因为归并排序的两种写法的 merge 部分是一样的，所以这里单独给出 merge 方法的实现如下：

/**
 * 将 data[l...mid] 和 data[mid + 1...r] 两部分进行归并
 * @param data 待排序数组
 * @param left 起始index
 * @param mid 中间index
 * @param right 结尾index
 */
private static void merge(int[] data, int left, int mid, int right) {
  // 用来辅助排序，保存合并后的序列
  int[] temp = new int[right - left + 1];
  // i，j，k的定义在上边已经介绍
  int i = left, j = mid + 1, k = 0;
  // 比较左右两个数组的元素
  while (i <= mid && j <= right) {
    temp[k++] = data[i] <= data[j] ? data[i++] : data[j++];
  }
  // 处理右边数组元素全部存进去，左边数组元素还没有存完的情况
  while (i <= mid) {
    temp[k++] = data[i++];
  }
  // 同上，处理左边数组元素全部存进去，右边数组元素还没有存完的情况
  while (j <= right) {
    temp[k++] = data[j++];
  }
  // 复制回原数组
  System.arraycopy(temp, 0, data, left, temp.length);
}

为了开拓大家的思路，下面再给出一种 merge 方法的实现如下：

/**
 * 将 data[l...mid] 和 data[mid + 1...r] 两部分进行归并
 * @param data 待排序数组
 * @param left 起始index
 * @param mid 中间index
 * @param right 结尾index
 */
private static void merge(int[] data, int left, int mid, int right) {
  int[] temp = Arrays.copyOfRange(data, left, right + 1);
  // i，j，k的定义在上边已经介绍
  int i = left, j = mid + 1;
  for (int k = left ; k <= right; k ++) {
    // 处理左边数组元素全部存进去，右边数组元素还没有存完的情况
    if (i > mid) {
      data[k] = temp[j - left];
      j ++;
    }
    // 处理右边数组元素全部存进去，左边数组元素还没有存完的情况
    else if (j > right) {
      data[k] = temp[i - left];
      i ++;
    }
    // 当前左边数组元素 < 当前右边数组元素
    else if (temp[i - left] < temp[j - left]) {
      data[k] = temp[i - left];
      i ++;
    }
    // 当前左边数组元素 >= 当前右边数组元素
    else {
      data[k] = temp[j - left];
      j ++;
    }
  }
}

归并排序优化

这里要讲两个小的优化点：

前面我们在分完组后直接进行 merge 操作，其实我们忽略了一种情况，那就是在分完组后 merge 之前，有可能两个数组已经就是有序的了，这时候就没必要再进行 merge 操作了。

具体在代码优化实现上，可以在 merge 之前加一个判断，判断如果 data[mid] > data[mid+1]，才进行 merge 操作。如果要处理的数据场景有可能会出现近乎有序的情况，我们可以加上这个优化。
第二个优化点要用到我们前面聊插入排序时的知识，在插入排序的最后，我们说到插入排序可以在更加复杂的排序算法中作为一个子过程来优化，便可以用在这里。

具体在代码优化实现上，可以在递归到数据量比较小时，转而使用插入排序提高性能。因为当数据量比较小的时候，插入排序会比归并排序快一些（此时整个数组近乎有序的概率也会比较大）。

不过，讲道理，虽然这两个优化点对归并排序的时间复杂度并没有影响，但是确实会让程序运行快一些。

归并排序优化代码

首先，需要对插入排序的代码进行一定的改写，要支持指定范围的插入排序，代码如下：

/**
 * 对data[l...r]的区间使用插入排序
 * @param data 待排序数组
 * @param l 起始index，代表left
 * @param r 结尾index，代表right
 */
private static void insertSort(int[] data, int l, int r){
  for( int i = l + 1 ; i <= r ; i ++ ){
    int e = data[i];
    int j = i;
    for (; j > l && data[j-1] > e; j--) {
      data[j] = data[j - 1];
    }
    data[j] = e;
  }
}

当然，归并排序的两种写法都可以用到上面提到的两个优化点（merge 代码同上）。

/**
 * mergeSort优化：Top-down；自顶向下；递归法
 * @param data 待排序数组
 */
public void mergeSort(int[] data){
  sort(data, 0, data.length - 1);
}

/**
 * sort
 * @param data 待排序数组
 * @param left 起始index
 * @param right 结尾index
 */
private static void sort(int[] data, int l, int r) {
  // 优化2: 对于小规模数组（这里指定为16个元素）, 使用插入排序
  if (r - l <= 15) {
    insertSort(data, l, r);
    return;
  }
  int mid = l + ((r - l) >> 1);
  sort(data, l, mid);
  sort(data, mid + 1, r);
  // 优化1
  if (data[mid] > data[mid+1]) {
    // merge 代码同上
    merge(data, l, mid, r);
  }
}

/**
 * mergeSort优化：Bottom-up；自底向上；非递归；迭代法
 * @param data 待排序数组
 */
public void mergeSort(int[] data){
  int n = data.length;
  // 优化2: 对于小规模数组（这里指定为16个元素）, 使用插入排序
  for (int i = 0; i < n; i += 16) {
    insertSort(data, i, Math.min(i + 15, n - 1));
  }
  for (int i = 16; i < n; i *= 2) {
    for (int j = 0; j < n - i; j += 2 * i) {
      // 优化1
      if (data[j + i - 1] > data[j + i]) {
        // merge 代码同上
        merge(data, j, j + i - 1, Math.min(j + 2 * i - 1, n - 1));
      }
    }
  }
}

复杂度和稳定性分析

大家可能都了解过，归并排序的时间复杂度为 O(n * logn)，那么它是怎么计算的呢？大致如下：

首先计算分组后的层数。会发现：如果数组有 n 个元素，那么层数就为 logn。如果 n 不是 2 的次方也没有关系，因为此时 logn 的结果是个浮点数，上取整即可。

接下来要分析 merge 的时间复杂度。会发现：虽然我们把它分成了不同的部分，但是每一层要处理的元素个数都是一样的。那么如果整个过程能够用 O(n) 的时间复杂度来解决，那么我们代码的时间复杂度就为 O(n * logn) 级别。而我们实现的 merge 操作时间复杂度就是 O(n)。

时间复杂度

最优时间复杂度：O(n * logn)
最坏时间复杂度：O(n * logn)
平均时间复杂度：O(n * logn)

空间复杂度：O(n)

前面已经分析过了，需要开辟临时空间来辅助完成 merge 过程。

归并排序是一种稳定排序。

凑字数

所谓慢工出细活，这篇文章写了两天，如果你看到这里了，能告诉我这篇文章对得起“通篇都是干货”这句话吗。

希尔排序

发表于 2020-04-21 分类于 algorithm 阅读次数： Disqus：

在上一篇介绍插入排序的文章末尾，我们说通过插入排序算法可以引申出另一个重要的排序算法-希尔排序（shell sort），这篇文章我们就来说说希尔排序。

希尔排序也称为递减增量排序算法。希尔排序的名称是以美国计算机科学家 Donald Lewis Shell 的名字来命名，本文就选了他本人作为封面，1959年7月他在ACM通讯（Communications of the ACM，CACM）上发表了希尔排序算法。

希尔排序思想

在上一篇插入排序的文章中提到两点：

在数组近乎有序的情况下，插入排序的性能非常高，甚至可以达到线性的排序效率；
在插入排序中，每次都和之前的一个元素进行比较。

希尔排序就是基于这两点提出了改进方法。首先明确，希尔排序有个“步长”的概念，我们记为 step。接下来看看希尔排序是怎么改进的：

通过 step 将数组中的数据分组，同组之间的数据进行独立排序（这里排序的方法用的其实就是插入排序），这样可以让一个元素一次性地移动 step 个位置，朝它的最终位置前进一大步；
将 step 逐渐缩小并进行排序，这样一步一步的将一个完全无序的数组变成一个近乎有序的数组；
最后当 step = 1 时，这时算法其实就变成了普通的插入排序，而数组此时也变成了近乎有序的数组，我们知道这种情况用插入排序会非常快。

可以发现，希尔排序的整体思路其实就是插入排序的延伸，而插入排序其实就是 step = 1 的希尔排序。

接下来就用个简单的demo来演示一下整个过程吧。假设初始“步长”为数组长度，“步长”的计算方式为：step = 前一次step / 2，待排序数组如下：

第一轮比较和交换的详细过程为：
step = 4，数据分组情况如下（相同颜色为一组）：[2, 7, 3]，[5, 9]，[4, 1]，[8, 6]

（1）2 < 7，保持不变；5 < 9，保持不变；4 > 1，交换位置

（2）8 > 6，交换位置

（3）7 > 3，交换位置

至此，第一轮比较结束，可以发现分组后每个独立分组之间的元素都是有序的。

接下来每次新的一轮都要先更新 step = 前一次step / 2，具体的比较和交换过程和上面类似，就不赘述了。这里直接给出所有轮次的 step 和初始分组情况以及结果如下：
step = 4；[2, 7, 3]，[5, 9]，[4, 1]，[8, 6]

step = 2；[2, 1, 3, 4, 7]，[5, 6, 9, 8]

step = 1；[1, 5, 2, 6, 3, 8, 4, 9, 7]

希尔排序代码

/**
 * shellSort
 * @param data 待排序数组
 * @return 排序后的数组
 */
private int[] shellSort(int[] data) {
  int len = data.length, e, j, before;
  // 第一层循环控制每轮的步长
  for (int step = len / 2; step >= 1; step /= 2) {
    // 细心的同学肯定会发现：下面两层 for 循环的代码，当 step = 1 时，其实就是插入排序的代码
    // 这里直接用插入排序的优化版来写。当然也可以继续改写成用二分查找优化的版本（插入排序文章中已经介绍，有兴趣的同学可以自己改写）
    for (int i = step; i < len; i++) {
      e = data[i];
      for(j = i; (before = j - step) >= 0 && data[before] > e; j = before) {
        data[j] = data[before];
      }
      data[j] = e;
    }
  }
  return data;
}

希尔排序优化

在某些极端情况下，希尔排序是比插入排序还要慢的。比如下面这种情况，仍然假设初始“步长”为数组长度，“步长”的计算方式为：step = 前一次step / 2，待排序数组如下：

按照之前的思路来分析，会发现，第一轮 step = 4 和第二轮 step = 2 时，每个单独的分组内部的元素都没有进行任何交换，一直到 step = 1 时，数组才按照插入排序的方式进行排序。对于这样的数组，希尔排序反而白白增加了分组的成本。

造成这种情况的主要原因是：step 选择的不合适，因为我们使用的计算 step 的算法得到的“步长”是个等比序列，会出现了增量的盲区。所以，为希尔排序选择更有效的“步长”成为了优化的关键。

其实只要最终的步长为 1，那么任何步长序列都可以工作，因为当步长为 1 时，算法会变为普通插入排序，这就保证了数据一定会被排序。那如何选择更有效的“步长”呢？

其实这个问题我们不用太纠结，因为许多计算机科学家们提出了很多步长序列，其背后都有着复杂的推导过程。

这里介绍其中两种：

目前已知的最好步长序列。由Sedgewick提出的(1, 5, 19, 41, 109, …)，该序列的项来自 9 * 4 ^ i - 9 * 2 ^ i + 1 和 2 ^ (i + 2) * (2 ^ (i + 2) - 3) + 1 这两个算式。用这样步长序列的希尔排序比插入排序要快，甚至在小数组中比快速排序和堆排序还快；
在大数组中表现优异的步长序列。由斐波那契数列除去0和1将剩余的数以黄金分割比的两倍的幂进行运算得到的数列(1, 9, 34, 182, 836, 4025, 19001, 90358, 428481, 2034035, 9651787, 45806244, 217378076, 1031612713,…)

当然大家只需要了解即可，有兴趣的同学可以深究一下。

复杂度和稳定性分析

时间复杂度

最优时间复杂度：O(n)
- 类似于插入排序的最优时间复杂度分析。
最坏时间复杂度：O(n^2)
平均时间复杂度：根据步长序列的不同而不同。O(n * (logn)^2)

空间复杂度：O(1)

整个过程都是原地排序，并没有用到其它辅助的空间。

希尔排序是一种不稳定排序。

假如待排序数组为 [4, 4, 3, 5, 2]。其实也很好理解，虽然一次插入排序是稳定的，但在不同步长的插入排序过程中，相同的元素可能在各自的插入排序中被移动，就可能导致其稳定性被打乱。

插入排序

发表于 2020-04-20 分类于 algorithm 阅读次数： Disqus：

不吹不黑，不捧不踩，插入排序（insertion sort）是真的很重要。你不会到现在还以为O(n^2)级别的排序算法都一无是处吧？如果是的话，希望通过本文能够让你对这个观念有个新的认识。

插入排序思想

插入排序的思想其实也很简单，我先从一个简单的例子说起。还记得本文的封面图是什么吗？嗯，扑克牌。大家肯定都玩过扑克牌，我们从牌桌上一张一张拿起扑克牌，然后在手里将扑克牌按照大小顺序插入到合适的位置，其实这整个过程大体上就是插入排序的思想。

再正式点的描述一下插入排序的思想，就是通过构建有序序列，对于未排序的数据，在已排序序列中从后向前扫描，找到相应位置并插入。

接下来就用个简单的demo来演示一下整个过程吧。待排序数组如下：

比较和交换的详细过程为：
（1）从数组第二个位置向前寻找插入的位置（为什么不从第一个位置开始？因为第一个数字自己本身可以认为就是有序的），5 > 2，保持不变
（2）从数组第三个位置向前寻找插入的位置，4 < 5，交换位置；4 > 2，保持不变

（3）从数组第四个位置向前寻找插入的位置，8 > 5，保持不变
（4）从数组第五个位置开始向前寻找插入的位置，7 < 8，交换位置；7 > 5，保持不变

（5）从数组第六个位置向前寻找插入的位置，3 < 8，交换位置；3 < 7，交换位置；3 < 5，交换位置；3 < 4，交换位置；3 > 2，保持不变

（6）从数组第七个位置向前寻找插入的位置，1 < 8，交换位置；1 < 7，交换位置；1 < 5，交换位置；1 < 4，交换位置；1 < 3，交换位置；1 < 2，交换位置

（7）从数组第八个位置向前寻找插入的位置，6 < 8，交换位置；6 < 7，交换位置；6 > 5，保持不变

至此，整个插入排序过程结束。

插入排序代码

/**
 * insertionSort
 * @param data 待排序数组
 * @return 排序后的数组
 */
private int[] insertionSort(int[] data) {
  // swap 时用到的临时变量
  int temp;
  // 从第 1 个元素开始遍历，因为第 0 个元素自己本身就是有序的
  for (int i = 1; i < data.length; i++) {
    // 从第 j 个位置开始往前遍历，寻找插入位置
    for (int j = i; j > 0 && data[j] < data[j - 1]; j--) {
      // swap
      temp = data[j];
      data[j] = data[j - 1];
      data[j - 1] = temp;
    }
  }
  return data;
}

插入排序优化

比较上面版本的插入排序代码和上一篇介绍的选择排序代码，我们会发现它们两个都是外循环嵌套内循环，而且插入排序在内循环中是会提前结束的，所以按理说插入排序应该更快一些。

其实不然，在某些情况下，上面版本的插入排序是比选择排序慢的。这是为什么呢？大家不要忽略了，虽然插入排序在内循环中会提前结束，但是插入排序还有交换元素的代价，这个操作可比比较元素大小还要耗时。

所以，我们优化插入排序的思路也出来了，我们的目的就是要让插入排序也在内循环中只交换一次。

具体在代码优化实现上，我们需要在内循环中，先把要寻找正确位置的元素记录下来，然后总是将较大的元素向右移动，直到找到正确的位置然后插入该元素即可。具体思路如下图所示：

插入排序优化代码

/**
 * insertionSort
 * @param data 待排序数组
 * @return 排序后的数组
 */
public int[] insertionSort(int[] data) {
  // e 为我们要为其寻找插入位置的元素；j 为元素 e 最终应该插入的位置
  int e, j;
  for (int i = 1; i < data.length; i++) {
    e = data[i];
    // 在寻找 e 插入位置的过程中，较大的元素向右移动
    for (j = i; j > 0 && data[j - 1] > e; j--) {
      data[j] = data[j - 1];
    }
    // 将 e 插入正确的位置
    data[j] = e;
  }
  return data;
}

插入排序再优化

实际上，插入排序还可以再优化。熟悉二分查找的同学肯定就想到了，因为数组前面都是有序区，所以可以在有序区中采用二分查找来减少比较的次数，从而加快速度。

不过，这种算法其实可以认为是插入排序的一个变种，也被称为二分查找插入排序。

插入排序再优化代码

这里直接给出代码，不熟悉二分查找的同学可以预习一下，或者在后面的文章中我会再说说二分查找算法。

/**
 * insertionSort
 * @param data 待排序数组
 * @return 排序后的数组
 */
public int[] insertionSort(int[] data) {
  int e, left, right, mid;
  for (int i = 1; i < data.length; i++) {
    e = data[i];
    left = 0;
    right = i - 1;
    while (left <= right) {
      // 大家可以思考一下这里计算 mid 为什么不用 (left + right) / 2 ？
      // 其实是为了防止溢出，这里也是以前 jdk 底层实现二分查找的一个 bug，读者可以体会一下
      mid = left + ((right - left) >> 1);
      if (data[mid] > e) {
        right = mid - 1;
      } else {
        // 元素相同时，插入在后面的位置
        left = mid + 1;
      }
    }
    // 将插入位置后面的元素都后移一位
    System.arraycopy(data, left, data, left + 1, i - left);
    // 插入元素
    data[left] = e;
  }
  return data;
}

复杂度和稳定性分析

时间复杂度

最优时间复杂度：O(n)
- 当用优化后的插入排序代码进行排序时，如果待排序数组本来就是有序的，那么在内循环中，每次比较时都会发现当前元素的位置就是它在数组中的正确位置，直接结束内循环进入下一次循环。假定待排序数组长度为 n，那么最优时间复杂度即为 O(n)。
最坏时间复杂度：O(n^2)
平均时间复杂度：O(n^2)

空间复杂度：O(1)

整个过程都是原地排序，并没有用到其它辅助的空间。

插入排序是一种稳定排序。

深入理解插入排序

插入排序 vs 选择排序

插入排序和选择排序都属于O(n^2)级别的排序算法，两者的最大区别是：对于内循环，插入排序可以提前结束，而选择排序必须让内外层循环都完全执行完成。所以选择排序在任何情况下都是非常慢的。如果对选择排序的思想有点模糊的话，可以点击文章的底部链接再复习一下。

插入排序的重要性质

除了可以提前终止内循环外，插入排序还有一个非常重要的性质：在数组近乎有序的情况下，它的性能会非常高，甚至比后面要介绍的O(n * logn)级别的排序算法还要快。

正是因为这个性质，插入排序不仅可以在更加复杂的排序算法中作为一个子过程来优化（在后面说到归并排序和快速排序优化时会用到），而且还具有非常重要的实际意义。

很多时候，在实际应用中，我们处理的真实数据就是近乎有序的。比如日志，按理来说日志都是有序的，但是在生成日志时有可能因为某些错误或程序运行时间过长等原因，导致有几条无序的日志，这时如果使用插入排序来处理，性能会更好。

插入排序的引申

通过插入排序算法还可以引申出另一个重要的排序算法，希尔排序（shell sort），在后面的文章中也会说到。

最后一问，你还认为O(n^2)级别的排序算法都一无是处吗？

选择排序

发表于 2020-04-19 分类于 algorithm 阅读次数： Disqus：

选择排序（selection sort）在排序算法中也是比较基础的一个，来，一起看看。

选择排序思想

和冒泡排序的名字一样，它的名字也是足够直白的。“选择”两个字对于人生来说真算的上是一个比较艰难的字眼，不过在选择排序中不用担心，这里做选择没那么难。具体来说，我们可以把数组看作两部分，一部分为有序区，一部分为无序区，我们每次只需要在数组无序区中选择出指定的值，然后把它放到有序区，直到无序区没有元素（具体操作来说，只需要把有序区和无序区两个值的位置交换即可）。

那什么是指定的值？我也不是故意要用这个含糊其辞的说法，正所谓“命运只有一个，而人生却有多种选择”，在这里也有多种选择。对于这个值，我们可以选择无序区的最大值；也可以选择无序区的最小值；甚至可以既选择无序区的最大值，又选择无序区的最小值。其实最后一种选择相当于是对前两种选择的一种优化，在下面会说到。

当然不同的选择也会导致放到有序区的规则不同。这里以数组从小到大排序为例，假如数组前半段为有序区，后半段为无序区，那么每次需要在无序区中选择出最小值，将它放到有序区的末尾即可；假如数组前半段为无序区，后半段为有序区，那么每次需要在无序区中选择出最大值，将它放到有序区的开头即可。

接下来就用个简单的demo来演示一下整个过程吧。假如数组前半段为有序区，后半段为无序区，待排序数组如下：

比较和交换的详细过程为：
（1）记录数组第一个位置，从第二个位置开始一直到数组末尾，找到其中的最小值对应的位置，交换两元素位置

（2）接下来都以此类推，记录数组第二个位置，从第三个位置开始一直到数组末尾寻找最小值，交换位置；记录数组第三个位置，从第四个位置开始一直到数组末尾寻找最小值，交换位置...

接下来直接给出所有轮次的结果如下：

1	5	4	8	7	9	2	6	3
1	2	4	8	7	9	5	6	3
1	2	3	8	7	9	5	6	4
1	2	3	4	7	9	5	6	8
1	2	3	4	5	9	7	6	8
1	2	3	4	5	6	7	9	8
1	2	3	4	5	6	7	9	8
1	2	3	4	5	6	7	8	9

当然，假如数组前半段为无序区，后半段为有序区的情况，和上边的demo相似，就不赘述了。

选择排序代码

/**
 * 每次选择最小值
 * @param data 待排序数组
 * @return 排序后的数组
 */
public int[] selectionSort(int[] data) {
    // minIndex 为最小值的下标；temp为 swap 时用到的临时变量
    int minIndex, temp;
    for (int i = 0; i < data.length - 1; i++) {
        minIndex = i;
        // 找出最小值的下标
        for (int j = i + 1; j < data.length; j ++) {
            if (data[j] < data[minIndex]) {
                minIndex = j;
            }
        }
        // 如果找到的最小值下标不是 i，两位置元素交换位置
        if (minIndex > i) {
            // swap
            temp = data[i];
            data[i] = data[minIndex];
            data[minIndex] = temp;
        }
    }
    return data;
}

/**
 * 每次选择最大值
 * @param data 待排序数组
 * @return 排序后的数组
 */
public int[] selectionSort(int[] data) {
    int maxIndex, temp;
    for (int i = data.length - 1; i >= 0; i--) {
        maxIndex = i;
        for (int j = 0; j < i; j++) {
            if (data[j] > data[maxIndex]) {
                maxIndex = j;
            }
        }
        if (maxIndex < i) {
            // swap
            temp = data[i];
            data[i] = data[maxIndex];
            data[maxIndex] = temp;
        }
    }
    return data;
}

选择排序优化

在前面说选择排序思想时已经卖了这个关子，在这里具体说说是怎么回事。在上面的介绍中，每次我们在选择指定值时，只选择最小值或最大值，然后每次只交换一对元素，那怎么给它提速呢？当然很简单，那我们每次选两个值，既选择最小值，又选择最大值，把每次遍历交换的元素增加一个，这样自然是能够减少遍历的次数，让排序提点速。

具体在代码优化实现上，有个点需要注意一下。当选出最小值和最大值后进行位置交换时，如果先交换的是最小值的位置，那么此时可能有一种情况，就是最小值的位置上原本放的是数组中的最大值，这种情况下需要更新一下最大值所在的位置。

好像有点绕，举个例子来说一下，假如待排序数组为 [4, 2, 1, 3]，第一轮找到最小值为 1，最大值为 4，先交换最小值，4 和 1 交换位置，此时最大值 4 的位置被交换到了原来 1 的位置，这时要把最大值的位置更新为原来 1 的位置，然后再交换最大值。

选择排序优化代码

/**
 * 每次选择最小值和最大值
 * @param data 待排序数组
 * @return 排序后的数组
 */
public int[] selectionSort(int[] data) {
    int minIndex, maxIndex, temp;
    for (int left = 0, right = data.length - 1; left < right; left++, right--) {
        minIndex = left;
        maxIndex = right;
        for (int i = left; i <= right; i++) {
            if (data[i] < data[minIndex]) {
                minIndex = i;
            }
            if (data[i] > data[maxIndex]) {
                maxIndex = i;
            }
        }
        if (minIndex > left) {
            // swap left and minIndex first
            temp = data[left];
            data[left] = data[minIndex];
            data[minIndex] = temp;
            // 先交换的是最小值的位置，所以需要考虑如果最大值位置原本就在 left 位置时的情况
            // 如果是该情况，那么当最小值被交换后，最大值此时的位置为 minIndex
            if (left == maxIndex) {
                maxIndex = minIndex;
            }
        }
        if (maxIndex < right) {
            // swap right and maxIndex
            temp = data[right];
            data[right] = data[maxIndex];
            data[maxIndex] = temp;
        }
    }
    return data;
}

复杂度和稳定性分析

时间复杂度

最优时间复杂度：O(n^2)
- 当用优化后的选择排序代码进行排序时，虽然遍历的次数减少了一半，时间复杂度变为O(n/2 * n/2)，运行时间确实有所减少，但是省略常数后，它的算法时间复杂度仍然为O(n^2)级别。
最坏时间复杂度：O(n^2)
平均时间复杂度：O(n^2)

空间复杂度：O(1)

整个过程都是原地排序，并没有用到其它辅助的空间。

选择排序是一种不稳定排序。

这个应该很好举例，假如待排序数组为 [4, 3, 4, 1, 2]。

原地排序和稳定性的概念在从冒泡排序开始最后中有解释，就不赘述了。

从冒泡排序开始

发表于 2020-04-18 分类于 algorithm 阅读次数： Disqus：

冒泡排序（bubble sort）在排序算法中应该算是比较经典也比较简单的一个了，咱们就直入正题吧。

冒泡排序思想

其实它的名称都已经够直白了对吧，就是“冒泡”嘛。但是具体是怎么“冒”的呢？就是从数组中第一个位置开始，相邻元素两两比较大小，如果左边的元素大于右边的元素，则交换两元素的位置，否则，就保持它们在数组中的位置不变；然后再继续比较接下来相邻两元素的大小。

这样在经过每一轮比较和交换之后，最大的数字就会被移动到数组的最右边。类比一下汽水中的小气泡，如果把数组的左边看作汽水的瓶底，右边看作汽水的瓶口，数组中最大的数字每一轮都会像小气泡一样浮到了最上面，是不是裸眼3D效果都已经出来了。

接下来就用个简单的demo来演示一下整个过程吧。待排序数组如下：

第一轮比较和交换的详细过程为：
（1）2 < 5，保持不变；5 > 4，交换位置

（2）5 < 8，保持不变；8 > 7，交换位置

（3）8 < 9，保持不变；9 > 1，交换位置

（4）9 > 6，交换位置

（5）9 > 3，交换位置

至此，第一轮比较结束，可以发现，数组中的最大值 9 已经位于数组末尾。

后续的比较和交换过程与第一轮是一样的，就不赘述了，这里直接给出所有轮次的结果如下：

2	4	5	7	8	1	6	3	9
2	4	5	7	1	6	3	8	9
2	4	5	1	6	3	7	8	9
2	4	1	5	3	6	7	8	9
2	1	4	3	5	6	7	8	9
1	2	3	4	5	6	7	8	9
1	2	3	4	5	6	7	8	9
1	2	3	4	5	6	7	8	9

冒泡排序代码

/**
 * bubbleSort
 * @param data 待排序数组
 */
private int[] bubbleSort(int[] data) {
  // swap 时用到的临时变量
  int temp;
  for (int i = 0; i < data.length - 1; i++) {
    for (int j = 0; j < data.length - 1 - i; j++) {
      if (data[j] > data[j + 1]) {
        // swap
        temp = data[j];
        data[j] = data[j + 1];
        data[j + 1] = temp;
      }
    }
  }
  return data;
}

冒泡排序优化

经过前面的介绍，冒泡排序看起来还是挺简单的对吧，是的，但是一定程度上很简单也就意味着很粗暴，其实对于上个版本的实现来说，还是有很大的优化空间的。

仍然以上面的demo为例，我们直接去看所有轮次的结果，会发现其实在第六轮的时候数组已经排好序了，但是程序还是会兢兢业业的去执行第七轮和第八轮，所以这就是一个可以优化的点。

具体在代码优化实现上，我们可以加一个标志位来标记数组是否已经有序（或者也可以说，是用来标记数组中元素是否进行过交换）。

冒泡排序优化代码

/**
 * bubbleSort优化
 * @param data 待排序数组
 * 如果某一轮已经有序，则提前结束
 */
public int[] bubbleSort(int[] data) {
  int temp;
  // 标记是否有序
  boolean isSorted;
  for (int i = 0; i < data.length - 1; i++) {
    // 每一轮开始 isSorted 初始值都置为 true
    isSorted = true;
    for (int j = 0; j < data.length - 1 - i; j++) {
      if (data[j] > data[j + 1]) {
        // swap
        temp = data[j];
        data[j] = data[j + 1];
        data[j + 1] = temp;
        // 如果进行了交换，意味着数组还不是有序的，isSorted 置为 false
        isSorted = false;
      }
    }
    if (isSorted) {
      break;
    }
  }
  return data;
}

冒泡排序再优化

这里说冒泡排序还可以再优化，针对的是一种特殊的情况来说的。这种情况就是给定的待排序数组前半段是无序的，后半段是有序的。

再用个简单的demo来演示一下这种情况。待排序数组如下：

第一轮比较和交换的详细过程为：
（1）4 > 3，交换位置

（2）4 > 2，交换位置

（3）4 > 1，交换位置

（4）4 < 5，保持不变；5 < 6，保持不变；6 < 7，保持不变；7 < 8，保持不变；8 < 9，保持不变至此，第一轮比较结束。

后续的比较和交换过程与第一轮是一样的，就不赘述了，这里可以发现一个问题：其实数组后半段已经是有序的了，但是每一轮还是会再去比较大小，其实这是没有必要的。所以这也是一个可以优化的点。

具体在代码优化实现上，我们可以维护一个边界位置，在该边界位置前半段是无序数组，后半段是有序数组，在内循环中，只需要比较到该边界的位置即可。

冒泡排序再优化代码

/**
 * bubbleSort优化
 * @param data 待排序数组
 * 每一轮排序后，记录最后一次元素交换的位置，该位置即为无序数组和有序数组的边界位置
 */
private int[] bubbleSort(int[] data) {
  int temp;
  boolean isSorted;
  // 每次交换的位置
  int lastChangeIndex = 0;
  // 无序数组和有序数组的边界，内循环中每次只需比较到这里为止，第一轮边界值为数组最后一个值
  int sortBorder = data.length - 1;
  for (int i = 0; i < data.length - 1; i++) {
    isSorted = true;
    for (int j = 0; j < sortBorder; j++) {
      if (data[j] > data[j + 1]) {
        // swap
        temp = data[j];
        data[j] = data[j + 1];
        data[j + 1] = temp;
        isSorted = false;
        // lastChangeIndex 更新为每次交换的位置
        lastChangeIndex = j;
      }
    }
    // 此时 lastChangeIndex 表示每一轮中最后一次交换的位置，即此时无序数组和有序数组的边界值，将它赋值给 sortBorder
    sortBorder = lastChangeIndex;
    if (isSorted) {
      break;
    }
  }
  return data;
}

复杂度和稳定性分析

时间复杂度

最优时间复杂度：O(n)
- 在最理想的情况下，即待排序数组本来就是有序的，用上述冒泡排序优化代码来实现，其实我们只需要遍历 1 次就可以了。假定待排序数组长度为 n，那么最优时间复杂度即为 O(n)。
最坏时间复杂度：O(n^2)
平均时间复杂度：O(n^2)

空间复杂度：O(1)

整个过程都是原地排序，并没有用到其它辅助的空间。

冒泡排序是一种稳定排序。

这里牵扯到两个概念，也在这里顺便介绍一下：

原地排序：在排序过程中不需要辅助空间，直接利用原来待排序数组的存储空间来进行比较和交换。

稳定性：如果待排序数组中存在相同的元素，且在排序后这些相同元素之间的顺序与排序前的顺序一致，则称这种排序为稳定性排序；否则，则为不稳定性排序。

1	5	4	8	7	9	2	6	3
1	2	4	8	7	9	5	6	3
1	2	3	8	7	9	5	6	4
1	2	3	4	7	9	5	6	8
1	2	3	4	5	9	7	6	8
1	2	3	4	5	6	7	9	8
1	2	3	4	5	6	7	9	8
1	2	3	4	5	6	7	8	9

2	4	5	7	8	1	6	3	9
2	4	5	7	1	6	3	8	9
2	4	5	1	6	3	7	8	9
2	4	1	5	3	6	7	8	9
2	1	4	3	5	6	7	8	9
1	2	3	4	5	6	7	8	9
1	2	3	4	5	6	7	8	9
1	2	3	4	5	6	7	8	9

1	5	4	8	7	9	2	6	3
1	2	4	8	7	9	5	6	3
1	2	3	8	7	9	5	6	4
1	2	3	4	7	9	5	6	8
1	2	3	4	5	9	7	6	8
1	2	3	4	5	6	7	9	8
1	2	3	4	5	6	7	9	8
1	2	3	4	5	6	7	8	9

2	4	5	7	8	1	6	3	9
2	4	5	7	1	6	3	8	9
2	4	5	1	6	3	7	8	9
2	4	1	5	3	6	7	8	9
2	1	4	3	5	6	7	8	9
1	2	3	4	5	6	7	8	9
1	2	3	4	5	6	7	8	9
1	2	3	4	5	6	7	8	9

1	5	4	8	7	9	2	6	3
1	2	4	8	7	9	5	6	3
1	2	3	8	7	9	5	6	4
1	2	3	4	7	9	5	6	8
1	2	3	4	5	9	7	6	8
1	2	3	4	5	6	7	9	8
1	2	3	4	5	6	7	9	8
1	2	3	4	5	6	7	8	9

2	4	5	7	8	1	6	3	9
2	4	5	7	1	6	3	8	9
2	4	5	1	6	3	7	8	9
2	4	1	5	3	6	7	8	9
2	1	4	3	5	6	7	8	9
1	2	3	4	5	6	7	8	9
1	2	3	4	5	6	7	8	9
1	2	3	4	5	6	7	8	9