Yangsanity's Blog

Life was like a box of chocolates

0%

Float Double 部分源码解析

发表于 分类于 阅读次数： Disqus：

前几篇一直在说 IEEE 754 标准，搞明白了这个标准，再来看 java 中 Float.java 和 Double.java 的源码，很多变量和方法就能理解了。

1

Float 和 Double 都是继承了 Number 类并实现了 Comparable 接口。

Comparable 接口大家都熟悉，它只有一个 compareTo 方法，用来比较两个数值的大小。这个方法在 Float.java 和 Double.java 里都有实现，相关源码在下面会说到。

Number 类是个抽象类，里面一共 6 个方法，分别可以表示转换为基本类型 byte、 double、 float、 int、 long 和 short 的数值，但是转换的特定语义和转换细节是由子类实现来定义。

另外从 Number 类的类注释上也可以获得一个重要信息：转换可能会丢失关于数值总体大小的信息，可能会丢失精度，甚至可能返回与输入符号不同的结果。

Float 属性

这些属性都和前面介绍的 IEEE 754 标准有关，先回顾下第一篇文章中的总结：

形式 指数 小数部分
零 全为 0 全为 0
非规约形式 全为 0 大于 0 小于 1
规约形式 1 到 2ᵉ - 2（不全为 0 也不全为 1） 大于等于 1 小于 2
无穷 2ᵉ - 1（全为 1） 全为 0
NaN 2ᵉ - 1（全为 1） 非 0

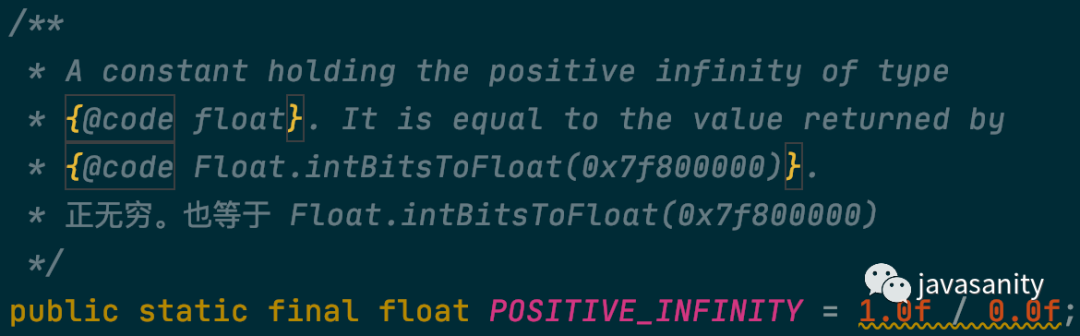
正无穷

二进制表示为：0 11111111 00000000000000000000000

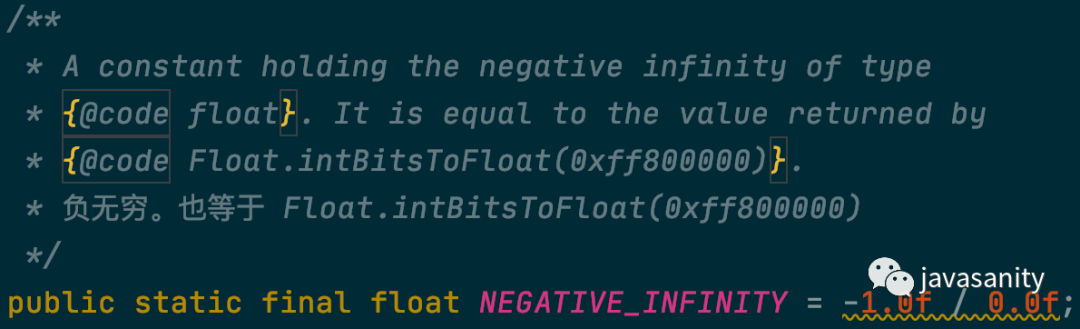
负无穷

二进制表示为：1 11111111 00000000000000000000000

NaN

二进制表示为：0 11111111 10000000000000000000000

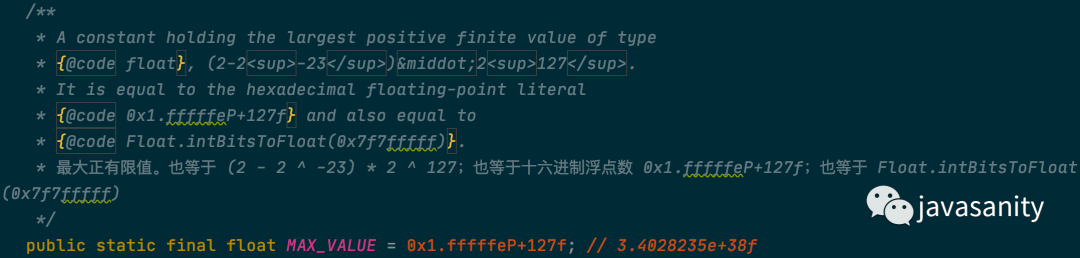
最大值

二进制表示为：0 11111110 11111111111111111111111

1
2
(1.11111111111111111111111)₂ * 2¹²⁷
= (2 - 2 ^ -23)₁₀ * 2¹²⁷

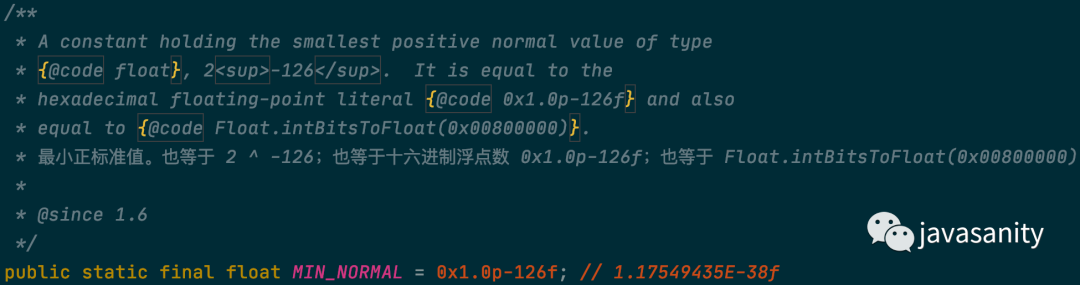
最小正标准值

二进制表示为：0 00000001 00000000000000000000000

其实就是第一篇介绍 IEEE 754 文章中提到的：大于 0 部分的规约形式浮点数的最小值。

最小值

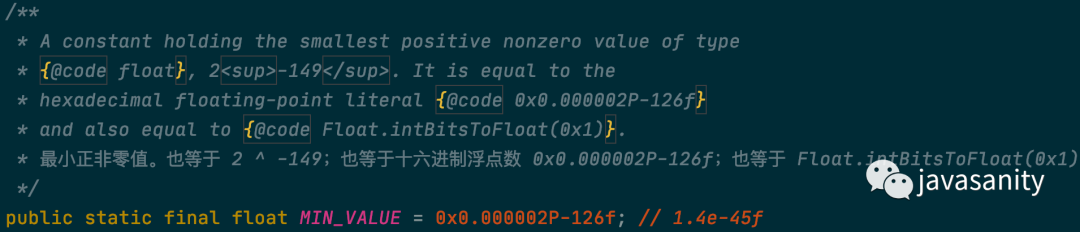
二进制表示为：0 00000000 00000000000000000000001

1
2
3
0.00000000000000000000001 * 2⁻¹²⁶
= 1 * 2⁻⁽¹²⁶⁺²³⁾
= 2⁻¹⁴⁹

其实就是第一篇介绍 IEEE 754 文章中提到的：大于 0 部分的非规约形式浮点数的最小值。

注意：虽然变量名叫 MIN_VALUE，但其实是个大于 0 的数。

最大指数

最小指数

位数

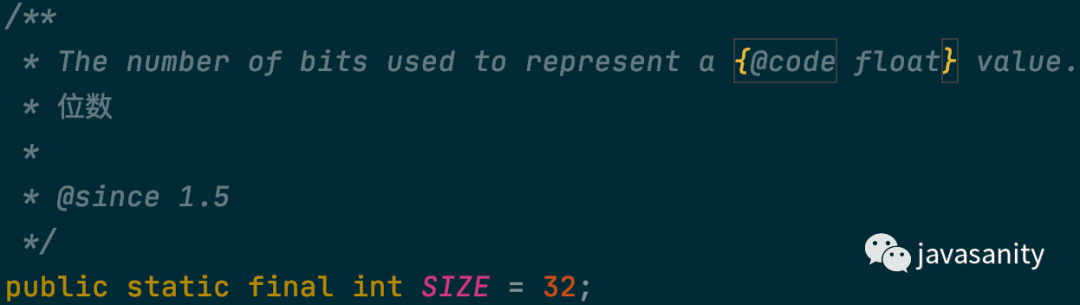
字节数

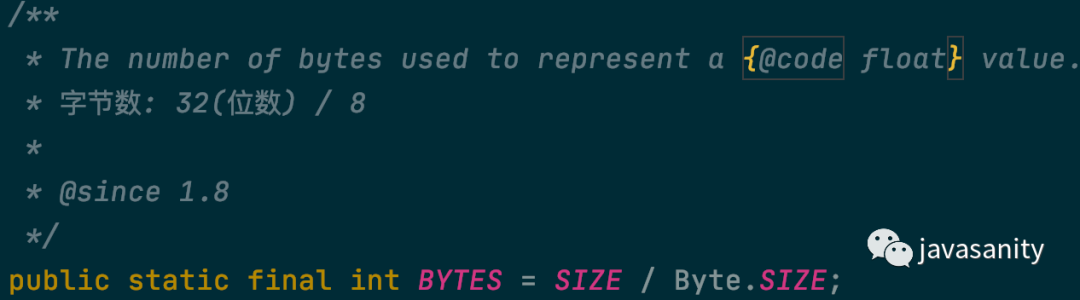
Float 方法

Float.floatToRawIntBits

是个 native 方法。它的作用是：将 float 浮点数转换为其 IEEE 754 标准二进制形式对应的 int 值。因为 float 和 int 都是 32 位，所以每一个 float 总有对应的 int 值。

如果参数为正无穷，则结果为 0x7f800000；如果参数为负无穷，则结果为 0xff800000；如果参数为 NaN，结果是表示实际 NaN 值的整数。

1
public static native int floatToRawIntBits(float value);

举两个例子大家就明白了：

  1. 1.0f

对应的二进制为 0 01111111 00000000000000000000000

那么 Float.floatToIntBits(1.0f) 的结果为：

1
2
2²³ + 2²⁴ + 2²⁵ + 2²⁶ + 2²⁷ + 2²⁸ + 2²⁹
= 1065353216
  1. -1.0f

对应的二进制为 1 01111111 00000000000000000000000

那么 Float.floatToIntBits(-1.0f) 的结果为：

1
2
3
2²³ + 2²⁴ + 2²⁵ + 2²⁶ + 2²⁷ + 2²⁸ + 2²⁹ + 2³¹
= 3212836864
= -1082130432

（不要忘了整数会溢出，所以最终结果为溢出后的值）

Float.floatToIntBits

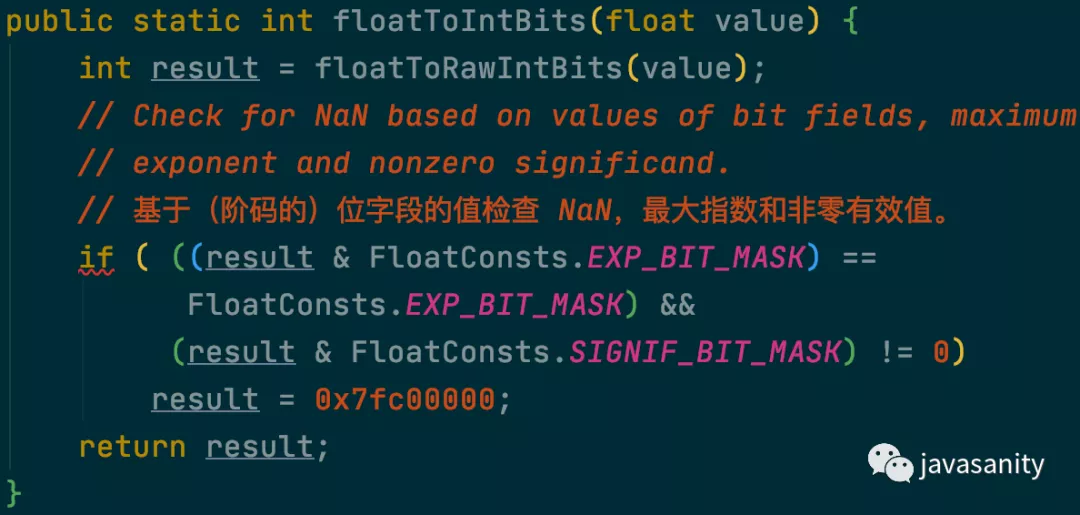
和 Float.floatToRawIntBits 方法几乎一样，唯一的区别是：对 NaN 作了检测，如果结果为 NaN，直接返回 0x7fc00000（即 Float.NaN）。

如果参数为正无穷，则结果为 0x7f800000；如果参数为负无穷，则结果为 0xff800000；如果参数为 NaN，则结果为 0x7fc00000。

前面的文章中介绍过，NaN 的阶码都为 1，尾数不全为 0，所以在 IEEE 754 标准中，NaN 并不是一个固定的值，而是一个范围。在 Java 中将 NaN 定义为了一个属性，在上边属性部分已经介绍过，它是一个固定的值。当结果处于 NaN 的范围中，此时会返回 Float.NaN 对应的值 0x7fc00000。

这一点在源码中也有体现。先调用 floatToIntBits 方法获取对应的 int 值，接下来检测 NaN，如果是 NaN，给返回值赋值为 0x7fc00000。

看看代码中是如何检测 NaN 的：

  • FloatConsts.EXP_BIT_MASK 是一个常量 2139095040，其对应的二进制表示为 0 11111111 00000000000000000000000

  • FloatConsts.SIGNIF_BIT_MASK 也是一个常量 8388607，其对应的二进制表示为 0 00000000 11111111111111111111111

  • 检测阶码：result & FloatConsts.EXP_BIT_MASK，如果 result 是 NaN，那么 result 的阶码都为 1，运算结果仍然为 FloatConsts.EXP_BIT_MASK

  • 检测尾数：result & FloatConsts.SIGNIF_BIT_MASK，如果 result 是 NaN，那么 result 的尾数不全为 0，运算结果肯定不为 0

  • 如果同时满足了这两个条件，那么 result 就是 NaN，给返回值赋值为 0x7fc00000

& 运算：1 & 1 = 1；0 & 1 = 0；1 & 0 = 0

Float.intBitsToFloat

是个 native 方法。它的作用是：返回与给定参数表示相对应的浮点值。可以这么理解，和 floatToIntBits 做的事情刚好相反（其实从方法名也能看出来）。

如果参数为 0x7f800000，则结果为正无穷；如果参数为 0xff800000，则结果为负无穷；如果参数值在 0x7f800001 到 0x7fffffff 或在 0xff800001 到 0xffffffff 之间，则结果为 NaN。

1
public static native float intBitsToFloat(int bits);

从它的方法注释上还能得到一些有用的信息，比如：

  1. Java 提供的任何 IEEE 754 浮点操作都不能区分具有不同位模式的两个同类型 NaN 值，不同的 NaN 值只能使用 Float.floatToRawIntBits 方法区分

  2. 根据参数如何求 s（符号位） e（阶码） m（尾数）：

1
2
3
int s = ((bits >> 31) == 0) ? 1 : -1;
int e = ((bits >> 23) & 0xff);
int m = (e == 0) ? (bits & 0x7fffff) << 1 : (bits & 0x7fffff) | 0x800000;

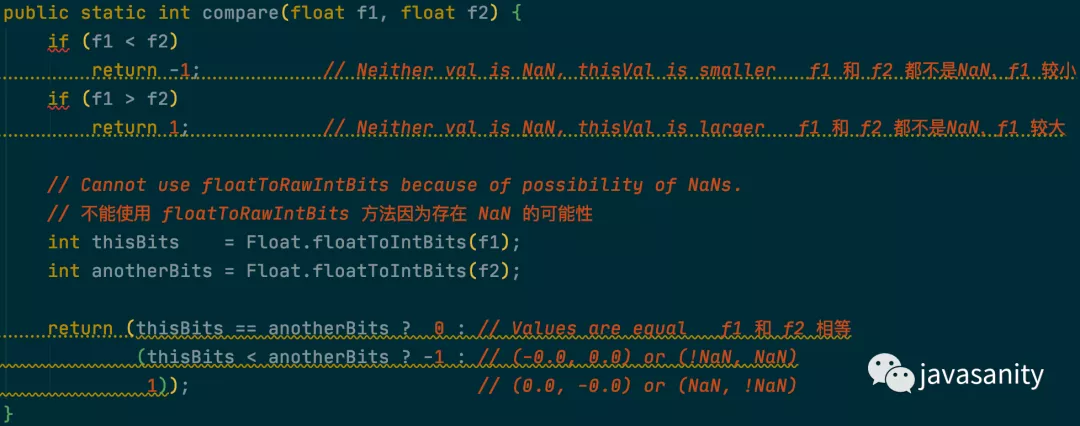
Float.compareTo

该方法直接调用了 Float.compare 方法，所以我们直接来看 compare 方法。

图中注释已经写的非常明白了，可以看到，两个浮点数的比较并不是想象中那么简单的，有一些特殊情况需要考虑。

Float.equals

Float.hashCode

重点是最后调用了 floatToIntBits 方法。

Float.isNaN

该方法直接调用了 isNaN(value) 方法，所以我们直接来看 isNaN(value) 方法，这个方法的判断逻辑也特别有意思。

可以看出，如果 v 为 NaN，则 v != v；如果 v 不为 NaN，则 v == v。

Double

同 Float，举一反三之。

欢迎关注我的其它发布渠道