浮点数的运算

这篇文章来看看浮点数是怎么进行四则运算的。

加减思路

首先来看两个十进制的小数如何进行相加和相减：

(1.6 * 10⁻⁵) + (0.3 * 10⁻⁶)
= (1.6 * 10⁻⁵) + (0.03 * 10⁻⁵)
= (1.6 + 0.03) * 10⁻⁵
= 1.63 * 10⁻⁵

(1.6 * 10⁻⁵) - (0.3 * 10⁻⁶)
= (1.6 * 10⁻⁵) - (0.03 * 10⁻⁵)
= (1.6 - 0.03) * 10⁻⁵
= 1.57 * 10⁻⁵

可以看到，两个十进制小数的加法或减法，要先做这一步：

(1.6 * 10⁻⁵) + (0.3 * 10⁻⁶) 
= (1.6 * 10⁻⁵) + (0.03 * 10⁻⁵)
或
(1.6 * 10⁻⁵) - (0.3 * 10⁻⁶) 
= (1.6 * 10⁻⁵) - (0.03 * 10⁻⁵)

原因很简单：两个小数相加，首先得把这两个数的小数点位置对齐。这么做的目的就是为了对齐小数点。然后就可以将相同的指数值作为公因数提出来，尾数再进行加减运算。

类比十进制，对于 IEEE 754 标准表示的二进制浮点数的加减运算，我们首先也要对齐小数点。从前面的文章我们知道，二进制浮点数其实也是科学计数法表示，要对齐小数点就要让两个浮点数科学计数法表示中的指数值相同，即要让两个浮点数的二进制表示中的阶码相同。这一步叫做对阶。

关于对阶，有个原则：小阶对大阶。意思就是指数小的浮点数的阶码要调整成指数大的浮点数的阶码。

这是因为对于二进制表示的浮点数来说，指数每升高一位，尾数就要右移一位，即尾数低位移出；反之，指数每降低一位，尾数就要左移一位，即尾数高位移出。相比之下，显然采用小阶对大阶损失的精度会更小，结果更准确。

所以，对阶的具体方法就是：小阶码加上大阶码和小阶码的差值，使之与大阶码相等，同时将小阶码对应的浮点数的尾数右移相应位数，以保证该浮点数的值不变（虽然还是避免不了损失一点精度）。

对阶之后，接下来进行尾数加减运算。

如果尾数进行加减运算后的结果是非规格化形式，需要依照 IEEE754 标准通过左规或右规来进行规格化操作（简单说就是转为 1.xxx * 2ⁿ 的形式）。

再多啰嗦一句，左规：尾数左移，阶码减值；右规：尾数右移，阶码加值。而右规操作一般只需将尾数右移一位即可，因为这种情况出现只会是尾数的最高位运算时出现了进位。

如果尾数过长，需要进行舍入处理。

浮点运算在对阶或右规时，尾数需要右移，被右移出去的位会被丢掉，从而造成运算结果精度的损失。为了减少这种精度损失，可以将一定位数的移出位先保留起来，在规格化后用于进行舍入处理。

关于这舍入处理，IEEE 754 标准给出了五种舍入规则：

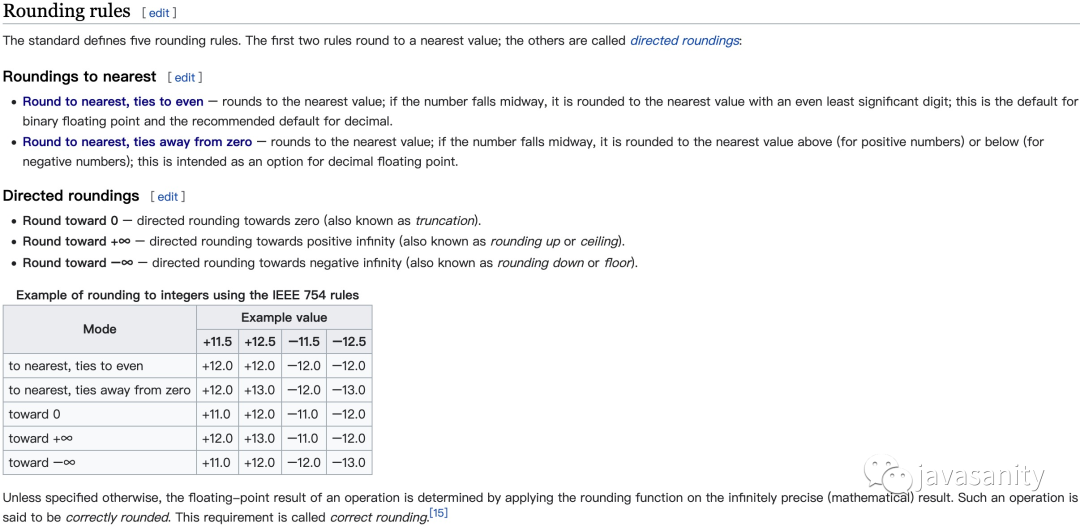
英文其实也不是很难，我用 Chrome 插件翻译了一下，中文有点不太准确，但是对照着应该也不耽误理解。。

对于二进制舍入，一般我们用 0 舍 1 入法（类似于十进制中的 4 舍 5 入法）即可，即溢出数的最高位为 0 则直接舍去，为 1 则前一位进 1。

（这跟上一篇文章中将 -36.35 转为单精度二进制的例子第四步是一样的，当时少说了这一嘴，直接给了结果）

最后就要对结果做溢出判断。浮点数的溢出是根据其运算结果后阶码的值是否产生溢出来判断的。

如果阶码的值超过了阶码所能表示的最大正数，则为上溢，进一步，若此时浮点数为正数，则为正上溢，记为 +∞，若浮点数为负数，则为负上溢，记为 -∞；如果阶码的值超过了阶码所能表示的最小负数，则为下溢，进一步，若此时浮点数为正数，则为正下溢，若浮点数为负数，则为负下溢。正下溢和负下溢都作为 0 处理。

至此，浮点数加减法的思路就说完了。

乘除思路

同样，先来看两个十进制的小数如何进行相乘和相除：

1
2
3

(1.2 * 10²) * (1.3 * 10³)
= (1.2 * 1.3) * 10²⁺³
= 1.56 * 10⁵

1
2
3

(1.2 * 10²) / (1.2 * 10³)
= (1.2 / 1.2) * 10²⁻³
= 1 * 10⁻¹

可以看到，相乘：尾数相乘，指数相加；相除：尾数相除，指数相减。

类比十进制，对于 IEEE 754 标准表示的二进制浮点数的乘除运算，也是类似的。

但是最终结果的阶码可不只是两个数阶码简单的直接相加或相减。

用单精度浮点数来举例子，假设 a 的阶码为 Ea，指数的实际值为 x，b 的阶码为 E𝖻，指数的实际值为 y。那么 Ea = x + 127，E𝖻 = y + 127。

a * b 需要 Ea + E𝖻，但是结果的阶码可不仅仅是 Ea + E𝖻，因为 Ea + E𝖻 = (x + 127) + (y + 127) = (x + y) + 254，看到问题了吧，所以最终结果的二进制阶码为 Ea + E𝖻 - 127。

a / b 需要 Ea - E𝖻，但是结果的阶码也不仅仅是 Ea - E𝖻，因为 Ea - E𝖻 = (x + 127) - (y + 127) = x - y，看到问题了吧，所以最终结果的二进制阶码为 Ea - E𝖻 + 127。

当然，最终结果的阶码也可以直接用 x 和 y 相加减后的结果加上 127 再转为二进制。

接下来，尾数运算，规格化，舍入处理，判断溢出都同上。

至此，浮点数乘除法的思路也说完了。

加法 example

例：计算 1.6 + 0.3

1 2	(1.6)₁₀ = (0 01111111 10011001100110011001101)₂ (0.3)₁₀ = (0 01111101 00110011001100110011010)₂

对阶

0.3 的阶码小，所以 0.3 的阶码调整为 01111111，对应尾数调整为：0.01001100110011001100110 10（最后的 10 先保留起来）

尾数运算

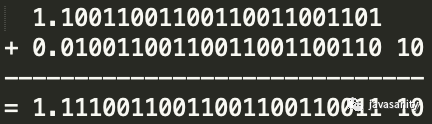
规格化，本例无需规格化
舍入处理

1.11100110011001100110011‬ 10 舍入处理后为 1.11100110011001100110100

所以最终尾数为：11100110011001100110100

溢出判断

没有溢出，所以最终结果为：(0 01111111 11100110011001100110100)₂

减法 example

1 2	(1.6)₁₀ = (0 01111111 10011001100110011001101)₂ (0.3)₁₀ = (0 01111101 00110011001100110011010)₂

例：计算 1.6 - 0.3

对阶，同上
尾数运算

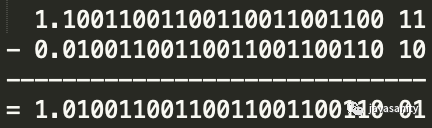
规格化，本例无需规格化
舍入处理

1.01001100110011001100110 01 舍入处理后为 1.01001100110011001100110

所以最终尾数为：01001100110011001100110

溢出判断

没有溢出，所以最终结果为：(0 01111111 01001100110011001100110)₂

乘法 example

例：*计算 1.5 * 0.3*

1 2	(1.5)₁₀ = (0 01111111 10000000000000000000000)₂ (0.3)₁₀ = (0 01111101 00110011001100110011010)₂

计算结果阶码

尾数运算

1 2	1.1 * 1.00110011001100110011010 = 1.110011001100110011001110

规格化，本例无需规格化
舍入处理

1.11001100110011001100111 0 舍入处理后为 1.11001100110011001100111

所以最终尾数为：11001100110011001100111

溢出判断

没有溢出，所以最终结果为：(0 01111101 11001100110011001100111)₂

除法 example

例：计算 1.5 / 0.3

1 2	(1.5)₁₀ = (0 01111111 10000000000000000000000)₂ (0.3)₁₀ = (0 01111101 00110011001100110011010)₂

计算结果阶码

尾数运算

1 2	1.1 / 1.00110011001100110011001 1001... = 1.01

规格化，本例无需规格化
舍入处理，本例也无需舍入

所以最终尾数为：01000000000000000000000

溢出判断

没有溢出，所以最终结果为：(0 10000001 01000000000000000000000)₂