leetcode之704-二分查找

之前在插入排序的文章中介绍了一个用二分查找来优化的思路，但是没有细说二分查找，今天也算是补上这个坑。刚好也是 leetcode 上的一道题。

二分查找算法（binary search algorithm），也称折半搜索算法（half-interval search algorithm）、对数搜索算法（logarithmic search algorithm）等。

思想

二分查找法是一种在有序数组中查找某一特定元素的搜索算法，它的思想比较简单：

从有序数组的中间元素开始搜索，如果中间元素正好是要查找的元素，则搜索过程结束；
如果要查找的元素大于或小于中间元素，则在数组大于或小于中间元素的那一半中进行查找，而且跟开始一样也从中间元素开始；
如果在某一步中数组为空，则代表要查找的元素不在数组中。

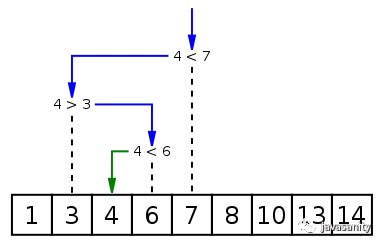
中间元素

二分查找每次都从有序数组的中间元素开始，那必然要先找到中间元素的索引值 mid。假设有序数组 nums 的第一个元素索引值记为 l，最后一个元素索引值记为 r，怎么求 mid 的值呢？

很简单，小学数学就学过：mid = (l + r) / 2。但是，在程序里可不一定是这样，前面在leetcode之7-整数反转的文章里我们知道，整数是有范围的。虽然 l 和 r 都是正常的整数，但是 l + r 就有可能会超过整数的范围，也就是说会有溢出的风险。

那如何安全的求两个整数的平均值呢？

（1）你可能会想了， (l + r) / 2 改成 l / 2 + r / 2 不就行了吗？在数学里确实是这样，但是我们讨论的是在程序里的情况。举个例子，l = 1，r = 3，那么 mid = 1 / 2 + 3 / 2 = 0 + 1 = 1，但其实正确结果应该是 2。

（2）换个角度来思考一下，既然我们知道了 l 和 r，那么我们给 l 加上 r - l 偏移量的一半不就行了，毕竟减法是不会溢出的。即 mid = l + (r - l) / 2。

（3）看看大师们是如何解决这个问题的。java 类库中也提供了二分搜索的方法，我们来看看源码中是怎样写的：mid = (l + r) >>> 1。

这么写就不怕 l + r 溢出了吗？不要震惊，仔细看后面是 >>> 1（无符号右移），而不是 >> 1（带符号右移），所以并没有问题。

其实也非常容易理解，如果我不把结果二进制的最高位当作符号来看，那溢不溢出又有什么关系呢？果然，大师的脑回路就是不一样。

注意事项

二分查找的思想比较简单，但是代码写起来却不太容易，因为有很多边界问题需要注意，所以我们一定要明确变量的含义，要记住一点：改变取值不代表改变含义。

举个例子，r 应该怎么取值？是取 nums.length 还是取 nums.length - 1 ？其实都可以，只是我们在写代码的过程中一定要注意不能改变 r 取值的含义。

非递归代码

定义要在 [l…r] 的范围里寻找 target，也就规定了 r = nums.length - 1。

值得一提的是，java 类库中提供的二分搜索用的就是这个定义。

/**
 * 在有序数组 nums 里查找元素 target
 * @param nums 有序数组
 * @param target 要查找的元素
 * @return 元素 target 的索引，如果没找到返回 -1
 */
public int binarySearch(int[] nums, int target){
    // 定义在 [l...r] 的范围里寻找 target（边界问题：r）
    int l = 0, r = nums.length - 1;
    // 当 l == r 时,区间 [l...r] 依然是有效的（边界问题：l < r or l <= r ？这就需要明确 l 和 r 的定义）
    while (l <= r) {
        int mid = (l + r) >>> 1;
        if (target > nums[mid]) {
            // 说明 target 在 [mid+1...r] 中（边界问题：l = mid or l = mid + 1 ？这就需要明确 l 和 r 的定义）
            l = mid + 1;
        } else if (target < nums[mid]) {
            // 说明 target 在 [l...mid-1] 中（边界问题：r = mid or r = mid - 1 ？这就需要明确 l 和 r 的定义）
            r = mid - 1;
        } else {
            return mid;
        }
    }
    return -1;
}

定义要在 [l…r) 的范围里寻找 target，也就规定了 r = nums.length。

/**
 * 在有序数组 nums 里查找元素 target
 * @param nums 有序数组
 * @param target 要查找的元素
 * @return 元素 target 的索引，如果没找到返回 -1 
 */
public int binarySearch(int[] nums, int target){
    // 定义在 [l...r) 的范围里寻找 target（边界问题：r）
    int l = 0, r = nums.length;
    // 当 l == r 时, 区间 [l...r) 是个无效区间（边界问题：l < r or l <= r ？这就需要明确 l 和 r 的定义）
    while (l < r) {
        int mid = (l + r) >>> 1;
        if (target > nums[mid]) {
            // 说明 target 在 [mid+1...r) 中（边界问题：l = mid or l = mid + 1 ？这就需要明确 l 和 r 的定义）
            l = mid + 1;
        } else if (target < nums[mid]) {
            // 说明 target 在 [l...mid) 中（边界问题：r = mid or r = mid - 1 ？这就需要明确 l 和 r 的定义）
            r = mid;
        } else {
            return mid;
        }
    }
    return -1;
}

递归代码

从二分查找思想的描述中，明显有一种递归的感觉，确实，二分查找也可以用递归的方式来写。这里同样给出两种不同定义的写法。

定义要在 [l…r] 的范围里寻找 target，也就规定了 r = nums.length - 1。

/**
 * 在有序数组 nums 里查找元素 target
 * @param nums 有序数组
 * @param target 要查找的元素
 * @return 元素 target 的索引，如果没找到返回 -1 
 */
public int binarySearch(int[] nums, int target){
    // 定义在 [l...r] 的范围里寻找 target
    return binarySearchHelp(nums, 0, nums.length - 1, target);
}

private int binarySearchHelp(int[] nums, int l, int r, int target) {
    // 边界问题, 同上
    if (l > r) {
        return -1;
    }
    int mid = (l + r) >>> 1;
    if (nums[mid] > target) {
        // 边界问题, 同上
        return binarySearchHelp(nums, l, mid - 1, target);
    } else if (nums[mid] < target) {
        // 边界问题, 同上
        return binarySearchHelp(nums, mid + 1, r, target);
    }
    return mid;
}

定义要在 [l…r) 的范围里寻找 target，也就规定了 r = nums.length。

/**
 * 在有序数组 nums 里查找元素 target
 * @param nums 有序数组
 * @param target 要查找的元素
 * @return 元素 target 的索引，如果没找到返回 -1 
 */
public int binarySearch(int[] nums, int target){
    // 定义在 [l...r) 的范围里寻找 target
    return binarySearchHelp(nums, 0, nums.length, target);
}

private int binarySearchHelp(int[] nums, int l, int r, int target) {
    // 边界问题, 同上
    if (l >= r) {
        return -1;
    }
    int mid = (l + r) >>> 1;
    if (nums[mid] > target) {
        // 边界问题, 同上
        return binarySearchHelp(nums, l, mid, target);
    } else if (nums[mid] < target) {
        // 边界问题, 同上
        return binarySearchHelp(nums, mid + 1, r, target);
    }
    return mid;
}

复杂度分析

时间复杂度：

二分查找每次比较都使搜索范围缩小一半（每次都除以 2），所以时间复杂度为 O(logn)。

空间复杂度：

对于非递归代码来说，没有使用额外的空间，所以空间复杂度为 O(1)；
对于递归代码来说，因为递归的次数和深度都是 logn，所以空间复杂度也为 O(logn)。

凑字数

二分查找法真是完美的说明了：思考一个算法的思想是简单的，但是写出一个没有 bug 的程序却是复杂的。