leetcode之9-回文数

有两点很明确：

负数不可能是回文数；
除了 0 以外，所有个位是 0 的数字不可能是回文数。

1

将数字本身反转，反转后的数字与原始数字进行比较，如果它们相同，那么这个数字就是回文数。

但是，要注意反转后的数字可能有溢出风险。不过上篇文章已经非常详细的介绍了溢出和反转数字应该怎么做。

public boolean isPalindrome(int x) {
    // 上述两种情况直接返回
    if (x < 0 || (x % 10 == 0 && x != 0)) {
        return false;
    }
    int copyx = x;
    // 翻转之后的数字可能超过整型的范围，用 long 来处理
    long y = 0;
    while (copyx != 0) {
        y = y * 10 + copyx % 10;
        copyx /= 10;
    }
    return x == y;
}

时间复杂度为 O(log(x))，因为 x 中大约有 lg(x) 位数字；空间复杂度为 O(1)。

2

将数字转换为字符串，通过对比字符串前后对称位置的字符是否相等来检查原始数字是否为回文。

有个可以优化的小点是我们只需遍历一半的字符串就够了。

public boolean isPalindrome(int x) {
    // 上述两种情况直接返回
    if (x < 0 || (x % 10 == 0 && x != 0)) {
        return false;
    }
    String str = String.valueOf(x);
    int n = str.length();
    for (int i = 0; i < n / 2; i++) {
        // 对比字符串前后对称位置的字符是否相等
        if (str.charAt(i) != str.charAt(n - 1 - i)) {
            return false;
        }
    }
    return true;
}

时间复杂度为 O(n / 2)，忽略常数后为 O(n)；空间复杂度为 O(n)，因为我们将数字转换为了字符串。

官方题解

一个非常巧妙的办法，反转一半的数字，这必然不会导致溢出。

其中我们要解决两个问题：

如何知道反转数字的位数已经达到原始数字位数的一半？
反转后的数字 revertedNumber 如何和原始数字 x 进行比较？

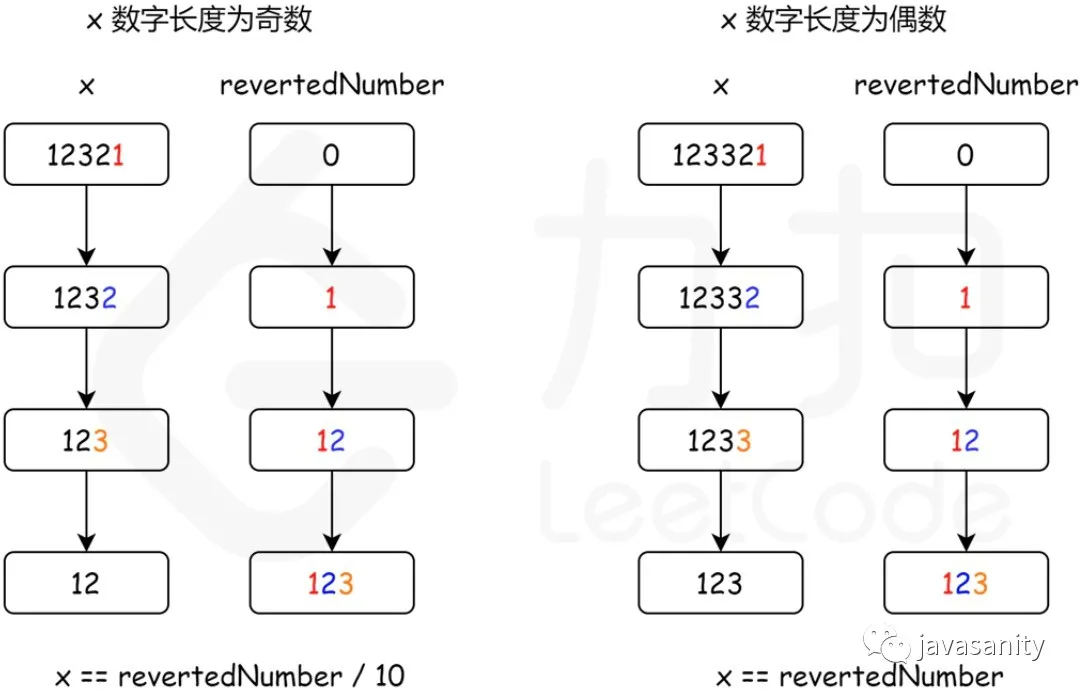
可以看到：

当原始数字 x 小于或等于反转后的数字 revertedNumber 时，就意味着已经处理了一半位数的数字了；
如果是回文数，最终 revertedNumber 和 x 的关系必然如上图所示。

public boolean isPalindrome(int x) {
    // 上述两种情况直接返回
    if (x < 0 || (x % 10 == 0 && x != 0)) {
        return false;
    }
    int revertedNumber = 0;
    // 反转一半
    while (x > revertedNumber) {
        revertedNumber = revertedNumber * 10 + x % 10;
        x /= 10;
    }
    // 判断是否回文
    return x == revertedNumber || x == revertedNumber / 10;
}

时间复杂度为 O(log(x))，因为 x 中大约有 lg(x) 位数字；空间复杂度为 O(1)。