Yangsanity's Blog

Life was like a box of chocolates

0%

二叉堆

发表于 分类于 阅读次数： Disqus：

按进度应该是要写堆排序的，所以这篇文章先来介绍一下堆（Heap）。

对于堆排序来说，排序反而是次要的，解决排序问题只是堆这种数据结构衍生出来的一个应用而已。

除此之外，堆还能衍生出来一个重要的数据结构-优先队列（Priority Queue），不过这个得后面再说。今天主要介绍堆的一种经典实现-二叉堆（Binary Heap）。

堆是树形结构，所以先简单复习几个树的概念。（只是解释二叉堆需要用到的几个概念而已）

二叉堆的形式

树（Tree）也是一种数据结构。二叉树（Binary Tree）是树的一种形式，二叉意味着每个节点最多只有两个孩子节点-左孩子结点和右孩子结点，当然“最多”这两个字也意味着，每个节点可以只有一个孩子节点或者没有孩子节点。从这个定义可以看出来，一个节点也可以称为一棵二叉树。

二叉树

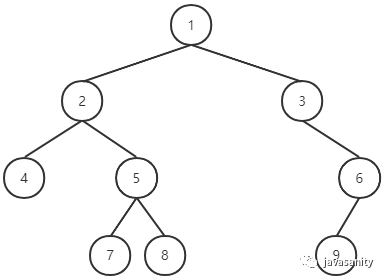
从图中可以看到两个规律：

  1. 二叉树的第 i 层至多拥有 2^(i - 1) 个节点；
  2. 深度为 h 的二叉树至多总共有 2^h - 1 个节点（根节点所在深度 0）。

二叉树有两种特殊形式，一种叫满二叉树（Full binary tree），一种叫完全二叉树（Complete Binary Tree）。

结合上面的规律，深度为 h 且节点总数为 2^h - 1 的二叉树为满二叉树。说直白点就是，如果一棵二叉树的所有非叶子节点都有左右孩子，并且所有叶子节点都在最后一层，则该二叉树为满二叉树。

满二叉树

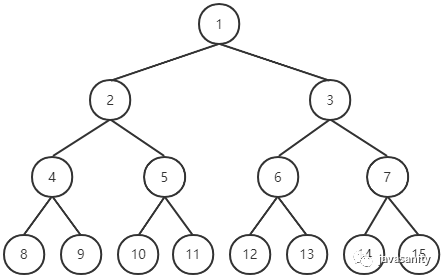
如果一棵二叉树除了最后一层节点之外，其它各层的节点个数都达到最大值，且最后一层的所有叶子节点是从左到右依次排布，则该二叉树为完全二叉树。

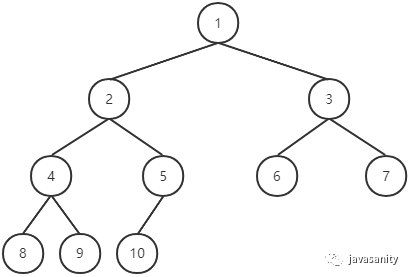
完全二叉树

说了这么多，就为了这一句：二叉堆本质上就是一颗完全二叉树。

二叉堆的类型

二叉堆可以分为两个类型：最大堆（大顶堆）和最小堆（小顶堆）。

二叉堆的根节点称为堆顶。最大堆中任何一个父节点的值都大于或等于它的左右孩子的节点的值；同理可得，最小堆中任何一个父节点的值都小于或等于它的左右孩子的节点的值。因此最大堆的堆顶元素是整个堆中的最大元素；最小堆的堆顶元素是整个堆中的最小元素。

但是有一点要强调一下，最大堆不意味着层数高的节点的数值一定大于层数低的节点的数值；最小堆也不意味着层数高的节点的数值一定小于层数低的节点的数值。

最大堆

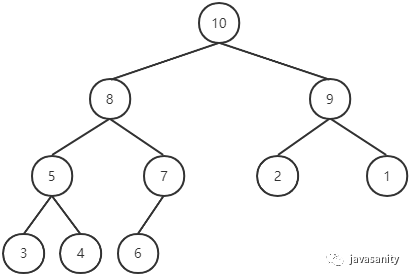
本文下面所有内容都以最大堆为例，最小堆可以留作大家的思考。

二叉堆（最大堆）的调整

二叉堆的调整一般有三种操作。

Shift Up（上浮）

向堆中插入一个元素。以上图中的堆插入一个新的元素 20 为例。插入位置为完全二叉树的最后一个位置。

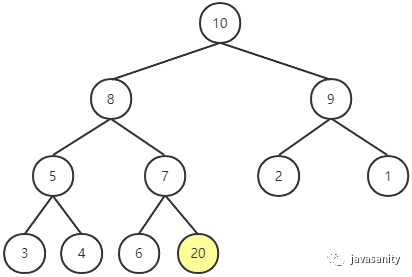
此时显然不符合最大堆的性质，所以对新插入节点做 Shift Up 操作：即用新插入节点的值和它父节点的值进行比较，如果大于父节点的值，则和父节点交换位置。

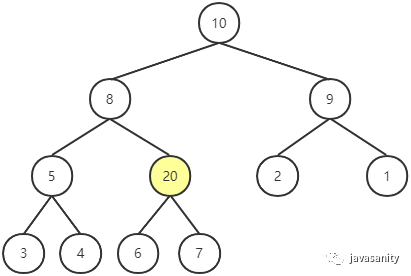
此时，发现还是不符合最大堆的性质，继续 Shift Up，直到满足最大堆的性质为止。

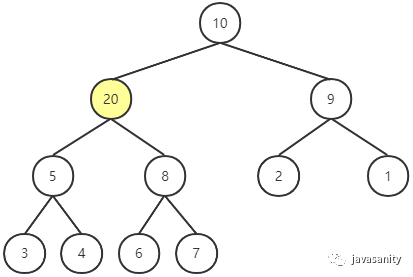
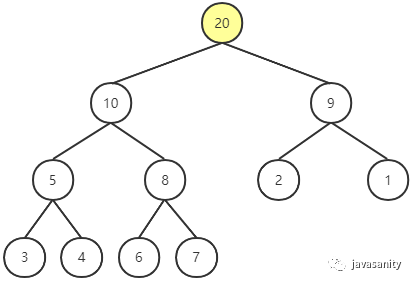
Shift Down（下沉）

从堆中删除一个元素。以上图中的堆删除一个元素为例。注意删除的元素只能是堆顶元素，此时，要把堆中的最后一个节点临时补到堆顶。

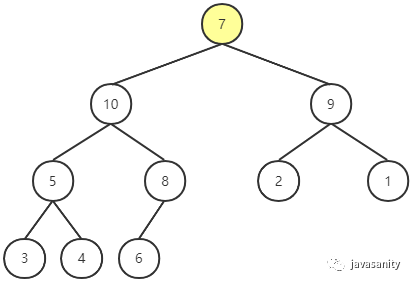
此时显然不符合最大堆的性质，所以对堆顶节点做 Shift Down 操作：即用堆顶节点的值和它左右孩子节点值中最大的一个（记为 p）进行比较，如果小于 p 节点的值，则和 p 节点交换位置。

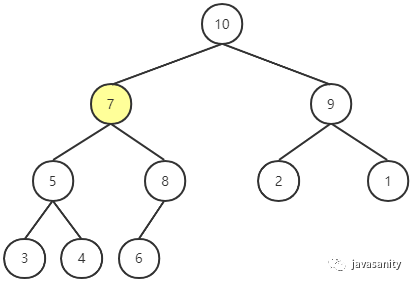
此时，发现还是不符合最大堆的性质，继续 Shift Down，直到满足最大堆的性质为止。

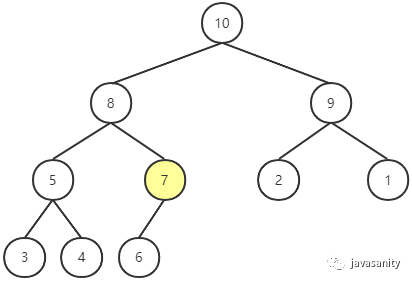
Heapify

将给定数组堆化，将数组变成一个最大堆。

这里先放一放，等了解完二叉堆的存储再来说 Heapify 的具体操作。

二叉堆（最大堆）的存储

既然二叉堆是一颗二叉树，那么它的代码实现自然是可以用常规的树的代码来实现。但是其实二叉堆的经典实现方式是数组。为什么可以用数组呢？正是因为二叉堆是一颗完全二叉树。我们把二叉树的节点值，按照自上到下，自左到右的顺序存到数组中。

一种经典的实现如下图所示：

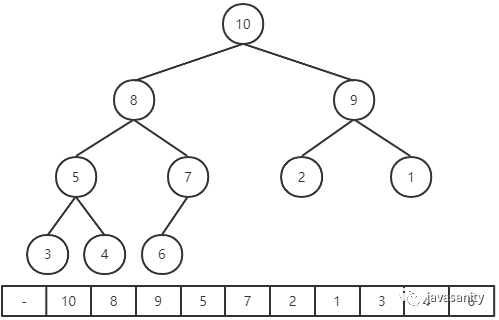
最大堆及其存储

可以看到我们从数组中的第二个索引位置开始放置元素，那么此时如何定位父节点和孩子节点之间的关系呢？可以依靠数组下标来计算。

这种实现的好处就是，节点之间的规律比较容易发现。假设 p 节点在数组中的索引位置为 i，那么对于 p 节点来说：

  1. parent(p) = i / 2
  2. leftChild(p) = 2 * i
  3. rightChild(p) = 2 * i + 1

但是这种实现会浪费索引为 0 的位置的空间，这简直是要逼死完美主义者（强迫症…）。所以这种实现思路就不给出具体的代码了，大家可以自己写一下。

其实我们也完全可以从 0 索引位置开始来存储，但是在规律上我们需要做一个大小为 1 的偏移量。

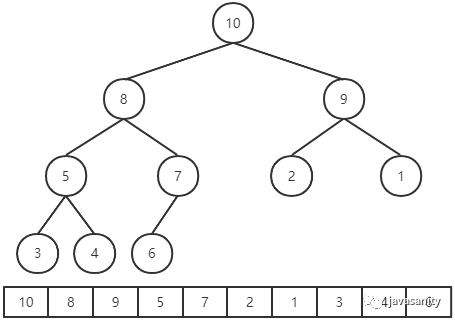
最大堆及其存储

此时的规律，假设 p 节点在数组中的索引位置为 i，那么对于 p 节点来说：

  1. parent(p) = (i - 1) / 2
  2. leftChild(p) = 2 * i + 1
  3. rightChild(p) = 2 * i + 2

再来说 Heapify

说到这里，我们再来想想，如何将给定数组堆化（最大堆）？

一个特别直观的思路就是，遍历这个数组，将每个元素都做 Shift Up 即可。在这个操作中，每个元素都要遍历一次，每次 Shift Up 都需要 logn 的时间，假设数组元素个数为 n，那么总的时间复杂度是 O(nlogn)。

其实 O(nlogn) 的时间复杂度已经非常不错了，但是其实还有一种更优的思路，只需要 O(n) 的时间复杂度。

这个思路就是，从最大堆的最后一个非叶子节点开始，向前遍历数组，每个元素依次做 Shift Down 操作即可。因为对于每个叶子节点来说，它们是符合最大堆的性质的。

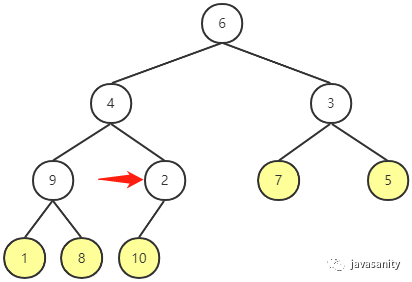
从最后一个非叶子节点开始向前遍历

这个思路的时间复杂度可能不太好证明，但是直观上来看，我们要将数组构建成最大堆，一上来就舍弃了数组中几乎一半的元素，那么速度肯定会更快。

现在唯一的问题就是最大堆的最后一个非叶子节点在数组中的索引是多少？不难发现，它的 index = (最后一个节点索引值 - 1) / 2。假设数组元素个数为 n，即 index = (n - 1 - 1) / 2 = (n - 2) / 2。

二叉堆（最大堆）代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
/**
 * 二叉堆，最大堆
 */
public class MaxHeap {

    /**
     * 二叉堆中存储的元素
     */
    private int[] data;

    /**
     * 二叉堆中存储的元素数量
     */
    private int count;

    /**
     * 二叉堆容量
     */
    private int capacity;

    public MaxHeap(int capacity) {
        this.data = new int[capacity];
        this.count = 0;
        this.capacity = capacity;
    }

    public MaxHeap(int[] data) {
        this(data, data.length);
    }

    public MaxHeap(int[] data, int len) {
        this.data = new int[len];
        this.capacity = len;
        this.count = len;
        System.arraycopy(data, 0, this.data, 0, data.length);
        // 从最后一个非叶子节点开始 shiftDown
        for (int i = (len - 2) / 2; i >= 0; i--) {
            shiftDown2(i);
        }
    }

    /**
     * 返回堆中的元素个数
     * @return 堆中的元素个数
     */
    public int size() {
        return count;
    }

    /**
     * 返回一个布尔值, 表示堆中是否为空
     * @return true 表示堆为空
     */
    public boolean isEmpty() {
        return count == 0;
    }

    /**
     * 堆中插入一个元素
     * @param i 插入的元素
     */
    public void insert(int i) {
        // todo 此处可以实现为动态扩容，会更友好些，大家可以自己去实现
        assert this.count < this.capacity;
        // 插入位置为堆的最后一个位置
        this.data[this.count] = i;
        // 对新插入节点做 shiftUp
        shiftUp2(this.count);
        this.count++;
    }

    private void shiftUp(int i) {
        // i 父节点的索引
        int ip;
        // i 不是根节点 && i 的父节点的值 < i 节点的值
        while (i > 0 && this.data[ip = (i - 1) / 2] < this.data[i]) {
            swap(i, ip);
            i = ip;
        }
    }

    // 优化 shiftUp，不一直swap
    private void shiftUp2(int i) {
        int e = this.data[i];
        // i 父节点的索引
        int ip;
        // i 不是根节点 && i 的父节点的值 < i 节点的值
        while (i > 0 && this.data[ip = (i - 1) / 2] < e) {
            this.data[ip] = this.data[i];
            i = ip;
        }
        this.data[i] = e;
    }

    /**
     * 获取堆中的最大值（从堆中删除一个元素）
     * @return 堆中最大值
     */
    public int getMax() {
        // todo 此处可以实现为动态扩容，会更友好些，大家可以自己去实现
        assert this.count >= 0;
        int ret = this.data[0];
        // 把堆中的最后一个节点临时补到堆顶
        swap(0, this.count - 1);
        this.count --;
        // 对新的堆顶节点做 shiftDown
        shiftDown2(0);
        return ret;
    }

    private void shiftDown(int i) {
        // il 代表 i 节点的左孩子节点索引；ir 代表 i 节点的右孩子节点索引
        int il, ir;
        // while (i 节点有左孩子)
        while ((il = 2 * i + 1) < this.count) {
            // j 是 i 节点的两个孩子节点中最大值的索引，初始值为左孩子的索引
            int j = il;
            // 如果 i 节点还有右孩子 且 右孩子的值大于左孩子的值，j 更新为右孩子的索引
            if ((ir = j + 1) < this.count && this.data[ir] > this.data[j]) {
                j = ir;
            }
            // 此时 data[j] 是 i 节点的两个孩子节点中的最大值
            // 如果 i 节点的值大于等于 data[j]，结束循环
            if(this.data[i] >= this.data[j]) {
                break;
            }
            swap(i, j);
            // 为下次循环做准备
            i = j;
        }
    }

    // 优化 shiftDown，不一直swap
    private void shiftDown2(int i) {
        int e = this.data[i];
        int il, ir;
        while ((il = 2 * i + 1) < this.count) {
            int j = il;
            if ((ir = j + 1) < this.count && this.data[ir] > this.data[j]) {
                j = ir;
            }
            if(e >= this.data[j]) {
                break;
            }
            this.data[i] = this.data[j];
            i = j;
        }
        this.data[i] = e;
    }

    /**
     * 交换堆数组中 i 和 j 索引位置的值
     * @param i 待交换索引
     * @param j 待交换索引
     */
    private void swap(int i, int j) {
        int temp = this.data[i];
        this.data[i] = this.data[j];
        this.data[j] = temp;
    }
}

（上面的代码中有两个小的优化，shiftUp2 和 shiftDown2，你看到了吗？）

凑字数

理解了二叉堆，堆排序就非常容易了，下一篇就可以直接开撕。

欢迎关注我的其它发布渠道