快速排序 part two

快排完结篇终于来了。

从上篇遗留问题说起

接着上篇最后留下的问题说：当待排序数组有非常多的重复值时，随着数据量增大，快排此时依然会退化到最坏时间复杂度 O(n^2)。为什么呢？

仍然从快排递归生成的递归树来考虑。当待排序数组有非常多的重复值时，上篇单路快排的 partition 操作还是会把整个数组分成极度不平衡的两部分。因为单路快排的 partition 方式会把等于基准值的数都放在基准值的某一边（左边或者右边）。如果待排序数组有大量重复元素，此时无论选择的基准值是什么，都会导致生成的递归树严重往一边倾斜。这种情况下，快排当然又会退化到最坏时间复杂度 O(n^2)。

双路快速排序思路

解决方案一：用双路快排的方式来重写 partition。

接下来用个简单的demo来演示一下整个过程吧。这里仍然规定直接简单选取数组第一个元素作为基准值，待排序数组如下：

5

3

9

5

2

4

5

8

1

首先我们必须定义几个变量来辅助我们理解整个过程。如下图，定义 pivot 为基准值；i 为从左往右正在遍历的元素；j 为从右往左正在遍历的元素。

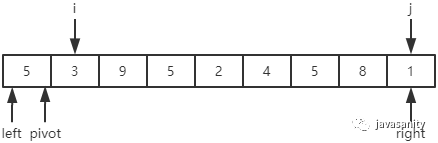
在整个遍历过程中，要一直保证 [left + 1, i - 1] 区间的元素都是小于等于基准值的，[j + 1, right] 区间的元素都是大于等于基准值的。

partition 过程为：

先从 i 开始向后扫描（或者，也可以先从 j 开始向前扫描），如果还没有遍历到 right 位置且当前值小于基准值，则不处理，继续查看下一个元素，直到找到一个值大于等于基准值；
这时从 j 开始向前扫描，如果还没有遍历到 left + 1 位置且当前值大于基准值，则不处理，继续查看下一个元素，直到找到一个值小于等于基准值；
此时，如果 i <= j，则交换 i 和 j 位置的值，之后 i 和 j 再分别指向下一个元素；否则跳出循环；
跳出循环后，现在应该把基准值放到合适的位置。那么这个位置是 i 还是 j 呢？分析一下：此时 i 的位置，是从前往后第一个大于等于基准值的元素；此时 j 的位置，是从后往前第一个（也就是从前往后最后一个）小于等于基准值的元素；而基准值是处在小于等于基准值的这一端，所以要将 pivot 和 j 位置的值进行交换即可。

第一轮 partition 的详细过程为：
（1）i：3 < 5，保持不变；9 > 5，停止；
j：1 < 5，停止；
i 和 j 位置的值进行交换，即 9 和 1 进行交换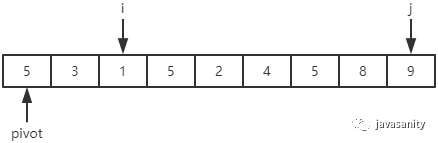

（2）i：5 = 5，停止；
j：8 > 5，保持不变；5 = 5，停止；
i 和 j 位置的值进行交换，即 5 和 5 进行交换（不要觉得这步多余哦）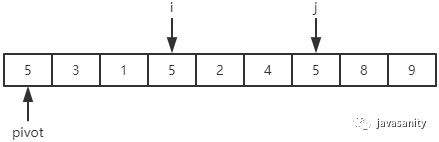

（3）i：2 < 5，保持不变；4 < 5，保持不变；5 = 5，停止；
j：4 < 5，停止；
此时 i > j，结束整个遍历过程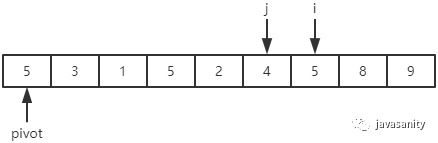

（4）遍历结束，把 pivot 和 j 位置的值进行交换，即 5 和 4 进行交换。此时，数组中所有小于等于 5 的元素都在它的左边，所有大于等于 5 的元素都在它的右边

4

3

1

5

2

5

5

8

9

（5）接下来只需要对 [4, 3, 1, 5, 2] 和 [5, 8, 9] 分别进行递归处理即可

第二步的最后，括号中写了不要觉得这一步多余，但是按理说，5 和 5 相等，交换也没有什么意义，直接跳过还能节省交换的时间，那么为什么还要进行交换呢？

从上一篇中我们知道，我们必须要保证排序过程中递归生成的递归树尽量平衡，才能避免快排的时间复杂度退化到 O(n^2)。第二步的交换操作正是为了这个原因。

举个例子，假如待排序数组为 [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]，如果 i 和 j 指向的 0 不进行交换，那么第一轮 partition 的结果是数组的第一个位置；如果交换，那么第一轮 partition 的结果是 4。可以看到，如果相同值不进行交换，会导致递归树平衡度不够好，从而影响排序性能。

双路快速排序代码

这里给出的代码也直接应用了上篇中提到的两个优化。

/**
 * quickSort双路快排
 * @param data 待排序的数组
 */
public void quickSort(int[] data) {
    quickSortHelper(data, 0, data.length - 1);
}

/**
 * 递归使用双路快排排序
 * @param data 待排序的数组
 * @param left 起始位置
 * @param right 结束位置
 */
private static void quickSortHelper(int[] data, int left, int right) {
    // 优化1：对于小规模数组（这里指定为16个元素）, 使用插入排序
    if(right - left <= 15){
        insertSort(data, left, right);
        return;
    }
    int pivot = partition(data, left, right);
    // 递归排序基准数左部分
    quickSortHelper(data, left, pivot - 1);
    // 递归排序基准数右部分
    quickSortHelper(data, pivot + 1, right);
}

/**
 * 对数组 [left, right] 部分进行 partition 操作，双路
 * @param data 待排序的数组
 * @param left 起始位置
 * @param right 结束位置
 * @return 返回基准值位置，保证 data[left...pivot - 1] < data[pivot]; data[pivot + 1...right] > data[pivot]
 */
private static int partition(int[] data, int left, int right) {
    // 优化2：随机在 data[left...right] 范围中, 选择一个位置作为基准值
    int randomIndex = (int) (Math.random() * (right - left + 1)) + left;
    int temp = data[left];
    data[left] = data[randomIndex];
    data[randomIndex] = temp;
    // pivot，i，j 的定义在上边已经介绍
    int pivot = data[left], i = left + 1, j = right;
    while (true) {
        while (i <= right && data[i] < pivot) {
            i++;
        }
        while (j >= left + 1 && data[j] > pivot) {
            j--;
        }
        if (i > j) {
            break;
        }
        // swap i and j
        temp = data[i];
        data[i] = data[j];
        data[j] = temp;
        i ++;
        j --;
    }
    // swap left and j
    data[left] = data[j];
    data[j] = pivot;
    return j;
}

/**
 * 为了方便大家观看，这个插入排序的代码是直接从上一篇中拿过来的
 * 对data[l...r]的区间使用插入排序
 * @param data 待排序数组
 * @param l 起始index，代表left
 * @param r 结尾index，代表right
 */
private static void insertSort(int[] data, int l, int r) {
  for( int i = l + 1 ; i <= r ; i ++ ){
    int e = data[i];
    int j = i;
    for (; j > l && data[j-1] > e; j--) {
      data[j] = data[j - 1];
    }
    data[j] = e;
  }
}

双路快速排序总结

回到最初的问题，我们再来分析一下为什么双路快排可以解决大量重复元素的问题。

对比上篇单路快排，双路快排的 partition 方式会把等于基准值的元素分散放在基准值的两边（左边和右边），所以生成的递归树平衡度就会好很多。因此在大量重复值的情况下，双路快排能够防止时间复杂度退化到 O(n^2)。

三路快速排序思路

解决方案二：用三路快排的方式来重写快排。

接下来用个简单的demo来演示一下整个过程吧。这里仍然规定直接简单选取数组第一个元素作为基准值，待排序数组如下：

5

3

9

5

2

4

5

8

1

同样，首先我们必须定义几个变量来辅助我们理解整个过程。如下图，定义 pivot 为基准值；i 为从左往右正在遍历的元素；lt（less than） 为小于基准值部分的最后一个元素；gt（greater than） 为大于基准值部分的第一个元素。

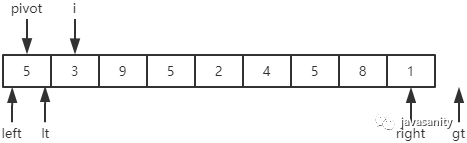
在整个遍历过程中，要一直保证 [left + 1, lt] 区间的元素都是小于基准值的，[gt, right] 区间的元素都是大于基准值的，[lt + 1, i - 1] 区间的元素都是等于基准值的，[i, gt) 是 i 要扫描的区间。

partition 过程为：

从 i 开始向后扫描，如果还没有遍历到 gt 位置，且当前值等于基准值，则不处理，继续查看下一个元素；
如果还没有遍历到 gt 位置，且当前值小于基准值，则交换 i 和 lt + 1 位置的值；然后 i 和 lt 都指向下一个元素；
如果还没有遍历到 gt 位置，且当前值大于基准值，则交换 i 和 gt - 1 位置的值；然后 gt 指向下一个元素。注意此时 i 是不用动的；
i 遍历结束后，再把 pivot 和 lt 位置的值进行交换即可。

第一轮 partition 的详细过程为：
（1）3 < 5，i 和 lt + 1 位置的值进行交换，即 3 不用动；然后 i 和 lt 都指向下一个元素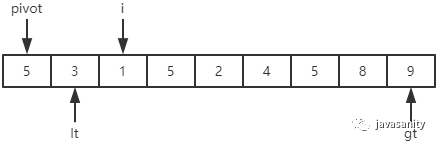

（2）9 > 5，i 和 gt - 1 位置的值进行交换，即 9 和 1 进行交换；然后 gt 指向下一个元素（注意此时 i 不用动）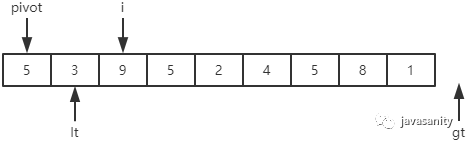

（3）（不要忘了 i 没有动）1 < 5，i 和 lt + 1 位置的值进行交换，即 1 不用动；然后 i 和 lt 都指向下一个元素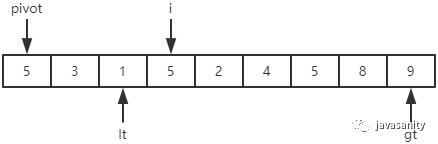

（4）5 = 5，保持不变；2 < 5，i 和 lt + 1 位置的值进行交换，即 2 和 5 进行交换；然后 i 和 lt 都指向下一个元素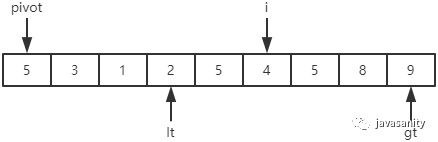

（5）4 < 5，i 和 lt + 1 位置的值进行交换，即 4 和 5 进行交换；然后 i 和 lt 都指向下一个元素；5 = 5，保持不变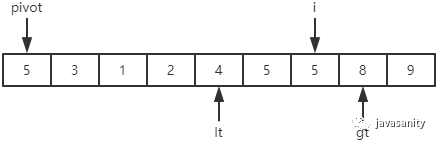

（6）遍历结束，把 pivot 和 lt 位置的值进行交换，即 5 和 4 进行交换。此时，数组中所有等于 5 的元素都位于数组中间，所有小于 5 的元素都在数组左边，所有大于 5 的元素都在数组右边

4

3

1

2

5

5

5

8

9

（7）接下来只需要对 [4, 3, 1, 2] 和 [8, 9] 分别进行递归处理即可

三路快速排序代码

这里给出的代码也直接应用了上篇中提到的两个优化。

/**
 * quickSort三路快排
 * @param data 待排序的数组
 */
private void quickSort(int[] data) {
    quickSortHelper(data, 0, data.length - 1);
}

/**
 * 递归使用三路快排排序
 * 直接包含了对数组 [left, right] 部分进行 partition 操作的代码
 * @param data 待排序的数组
 * @param left 起始位置
 * @param right 结束位置
 */
private static void quickSortHelper(int[] data, int left, int right) {
    // 优化1：对于小规模数组（这里指定为16个元素）, 使用插入排序
    if (right - left <= 15) {
        insertSort(data, left, right);
        return;
    }
    /* partition start */
    // 优化2：随机在 data[left...right] 范围中, 选择一个位置作为基准值
    int randomIndex = (int) (Math.random() * (right - left + 1)) + left;
    int temp = data[left];
    data[left] = data[randomIndex];
    data[randomIndex] = temp;
    // pivot，i，lt，gt 的定义在上边已经介绍
    int pivot = data[left], lt = left, gt = right + 1, i = left + 1;
    while (i < gt) {
        if (data[i] < pivot) {
            // swap i and lt + 1
            temp = data[i];
            data[i] = data[lt + 1];
            data[lt + 1] = temp;
            i ++;
            lt ++;
        } else if (data[i] > pivot) {
            // swap i and gt - 1
            temp = data[i];
            data[i] = data[gt - 1];
            data[gt - 1] = temp;
            gt --;
        } else {
            // if (data[i] == pivot)
            i ++;
        }
    }
    // swap left and lt
    data[left] = data[lt];
    data[lt] = pivot;
    /* partition end */
    // 递归排序数组左部分
    quickSortHelper(data, left, lt - 1);
    // 递归排序数组右部分
    quickSortHelper(data, gt, right);
}

/**
 * 为了方便大家观看，这个插入排序的代码是直接从上一篇中拿过来的
 * 对data[l...r]的区间使用插入排序
 * @param data 待排序数组
 * @param l 起始index，代表left
 * @param r 结尾index，代表right
 */
private static void insertSort(int[] data, int l, int r) {
  for( int i = l + 1 ; i <= r ; i ++ ){
    int e = data[i];
    int j = i;
    for (; j > l && data[j-1] > e; j--) {
      data[j] = data[j - 1];
    }
    data[j] = e;
  }
}

三路快速排序总结

为什么我们这次不是重写 partition，而是直接把 partition 的部分写在了 quickSortHelper 里呢？

相信大家也都明白了，对于三路快排的 partition 来说，不只是简单的返回索引位置，每次 partition 结束后中间部分都是一个区间，这就导致没办法把 partition 部分的代码再单独设计成一个函数了。

其实解决大量重复元素最经典的方式就是三路快排，这种方式在大量重复值的情况下效率更高。因为对比双路快排，三路快排会把数组分成小于基准值、等于基准值和大于基准值三部分，这样在每次 partition 结束后，等于基准值的部分就已经放到了数组正确的位置，在后续递归过程中这部分就不用再处理了，只需要再递归处理小于基准值和大于基准值的部分即可。

可以看到三路快排的优点是不需要对大量等于基准值的元素进行重复操作，如果等于基准值的元素非常多，在后续递归过程中就可以一次性少处理很多元素。所以在大量重复值的情况下，这个优化会非常明显。

复杂度和稳定性分析

1. 时间复杂度

• 最优时间复杂度：O(n * logn)

  • 分析过程可以类似于归并排序，都是分治法。

• 最坏时间复杂度：O(n^2)

• 平均时间复杂度：O(n * logn)

2. 空间复杂度：O(logn) ~ O(n)

• 我们的快排代码是通过递归调用实现的，所以需要一个栈空间来辅助递归。最好情况下，类似于归并排序，所需栈的最大深度为 logn；最坏情况下，所需栈的最大深度为 n。所以，快排的空间复杂度为 O(logn) ~ O(n)。

3. 快速排序是一种不稳定排序。

• 上面双路快排的 demo 已经能够说明。

凑字数

到此为止，终于把快排分析完了。感谢你看到了这里，希望文章能够对你有些帮助。如果再遇到快排相关面试的话，希望你能够侃侃而谈。

---