Yangsanity's Blog

Life was like a box of chocolates

0%

快速排序 part one

发表于 分类于 阅读次数： Disqus：

快速排序（quick sort）又称分区交换排序（partition-exchange sort），简称快排。它的鼎鼎大名，在排序界无人不知，无人不晓，重要性更是无需多言。毕竟敢叫这么直白的名字，那“实力”肯定也是没话讲的。

快排还有一个响亮的 title，它被称为20世纪对世界影响最大的算法之一。当然，它必须也是面试中算法的一个高频考察点。（必须要再次提到面试，原因你懂的）

我猜你可能知道单路快排，那么你知道还有双路快排吗？甚至三路快排吗？知道如何优化快排吗？废话不多说，赶快上车。

快速排序思想

和归并排序一样，快排也是使用了分治法（Divide and Conquer）的思想，把一个待排序数组以基准值为界，分为两个子数组，左边都比基准值小，右边都比基准值大，然后再递归地对两个子数组进行排序。

快排大概可以分为三个步骤：

  1. 从当前待排序的数组中选择一个元素作为基准值（pivot）；

  2. 把基准值移动到当数组排好序时它应该处于的正确位置上，并且使得数组中所有比基准值小的元素放在基准值左边，所有比基准值大的元素放在基准值右边（与基准值相等的数可以到任何一边）。这个操作一般称为 partition；

  3. 对基准数左边数组和右边数组再分别继续使用相同的思路进行排序，逐渐递归下去，直到完成整个排序过程。

单路快速排序思路

接下来用个简单的demo来演示一下整个过程吧。这里先规定直接简单选取数组第一个元素作为基准值，待排序数组如下：

5 8 2 4 7 9 1 6 3

首先我们必须定义几个变量来辅助我们理解整个过程。如下图，定义 pivot 为基准值；i 为当前正在遍历的元素；j 为小于基准值的区域边界。

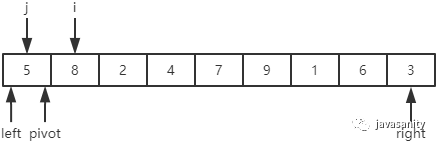
在整个遍历过程中，要一直保证 [left + 1, j] 区间的元素都是小于基准值的，[j + 1, i - 1] 区间的元素都是大于等于基准值的（这里把等于基准值的元素放到了 [j + 1, i - 1] 区间中，当然也可以放到 [left + 1, j] 区间中）。所以在遍历的过程中，只有当 i 当前指向的值小于 pivot 时，我们才需要把当前 i 位置的值和 j + 1 位置的值进行交换；当遍历完成时，再把 pivot 和 j 位置的值进行交换即可。

第一轮 partition 的详细过程为：

（1）8 > 5，保持不变；2 < 5，i 和 j + 1 位置的值进行交换，即 2 和 8 进行交换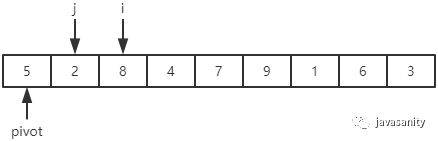

（2）4 < 5，i 和 j + 1 位置的值进行交换，即 4 和 8 进行交换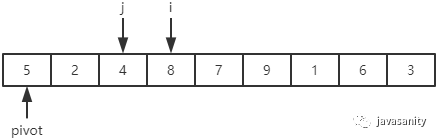

（3）7 > 5，保持不变；9 > 5，保持不变；1 < 5，i 和 j + 1 位置的值进行交换，即 1 和 8 进行交换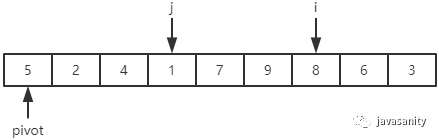

（4）6 > 5，保持不变；3 < 5，i 和 j + 1 位置的值进行交换，即 3 和 7 进行交换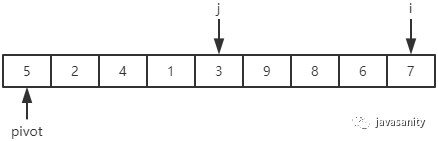

（5）此时，遍历完成，把 pivot 和 j 位置的值进行交换，即 5 和 3 进行交换。此时，数组中所有比 5 小的元素都在它的左边，所有比 5 大的元素都在它的右边

3 2 4 1 5 9 8 6 7
（6）接下来，对 5 左右两边的数组再分别继续使用相同的方法进行排序，直到完成整个排序过程。

注：上面是从左到右使用单路快排的思路，为了开拓思维，当然也可以使用从右到左单路快排的思路。

单路快速排序代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * quickSort单路快排
 * @param data 待排序的数组
 */
public void quickSort(int[] data) {
  quickSortHelper(data, 0, data.length - 1);
}

/**
 * 递归使用单路快排排序
 * @param data 待排序的数组
 * @param left 起始位置
 * @param right 结束位置
 */
private static void quickSortHelper(int[] data, int left, int right) {
  if (left >= right) {
      return;
  }
  int pivot = partition(data, left, right);
  // 递归排序基准数左部分
  quickSortHelper(data, left, pivot - 1);
  // 递归排序基准数右部分
  quickSortHelper(data, pivot + 1, right);
}

/**
 * 对数组 [left, right] 部分进行 partition 操作，从左往右单路
 * @param data 待排序的数组
 * @param left 起始位置
 * @param right 结束位置
 * @return 返回基准值位置，保证 data[left...pivot - 1] < data[pivot]; data[pivot + 1...right] > data[pivot]
 */
private static int partition(int[] data, int left, int right) {
  // pivot，i，j的定义在上边已经介绍
  int pivot = data[left], j = left, temp;
  for (int i = left + 1 ; i <= right; i ++) {
      if (data[i] < pivot) {
          j++;
          // swap i and j + 1
          temp = data[j];
          data[j] = data[i];
          data[i] = temp;
      }
  }
  // swap left and j
  data[left] = data[j];
  data[j] = pivot;
  return j;
}

单路快速排序优化

首先第一个优化相信大家看了上一篇归并排序优化的话肯定能想到，那就是当递归到数据量比较小时，转而使用插入排序提高性能。

除此之外，其实这里还有一个非常重要的问题：如果当待排序数组是近乎有序或者完全有序的情况下，会发生什么事情？

大家可以在自己的 ide 上测试一下，会发现，当随着数据量增大，快排会越来越慢。这是为什么呢？

我们对比着归并排序来分析一下。归并排序和快速排序都是使用的分治法的思想，都是要把待排序数组一分为二，不同的是，归并排序能保证每次都是把数组平均一分为二，而快排是以基准值一分为二，所以一般情况下，快排分出来的子数组都是一大一小的。

所以对于两者递归生成的递归树，归并排序的平衡度要更好，并且可以保证递归树的高度为logn，而快排生成的递归树高度非常有可能要比logn高。最差情况就是当整个待排序数组本来就近乎有序或者完全有序时，此时快排的时间复杂度会退化到最坏的时间复杂度 O(n^2)。

一句话概括造成这种情况的原因，就是基准值选的不够好。不能简单粗暴的直接选数组中第一个值作为基准值，我们希望的最好情况是能够选择数组排好序时中间的元素作为基准值。可是这个值又不好准确的定位，其实，我们只需要在数组中随机选择一个元素即可。

在这种情况下，快排的时间复杂度退化为 O(n^2) 的可能性是非常非常低的，几乎为 0。

具体在代码优化实现上，我们只需要在上边 partition 代码开始时加一行代码，把 left 和随机位置的值进行交换即可，后边的代码都不用动。

单路快速排序优化代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
/**
 * quickSort单路快排优化
 * @param data 待排序的数组
 */
public void quickSort(int[] data) {
  quickSortHelper(data, 0, data.length - 1);
}

/**
 * 递归使用单路快排排序
 * @param data 待排序的数组
 * @param left 起始位置
 * @param right 结束位置
 */
private static void quickSortHelper(int[] data, int left, int right) {
    // 优化1：对于小规模数组（这里指定为16个元素）, 使用插入排序
    if(right - left <= 15){
        insertSort(data, left, right);
        return;
    }
    int pivot = partition(data, left, right);
    // 递归排序基准数左部分
    quickSortHelper(data, left, pivot - 1);
    // 递归排序基准数右部分
    quickSortHelper(data, pivot + 1, right);
}

/**
 * 对数组 [left, right] 部分进行 partition 操作，从左往右单路
 * @param data 待排序的数组
 * @param left 起始位置
 * @param right 结束位置
 * @return 返回基准值位置，保证 data[left...pivot - 1] < data[pivot]; data[pivot + 1...right] > data[pivot]
 */
private static int partition(int[] data, int left, int right){
    // 优化2：随机在 data[left...right] 范围中, 选择一个位置作为基准值
    int randomIndex = (int) (Math.random() * (right - left + 1)) + left;
    int temp = data[left];
    data[left] = data[randomIndex];
    data[randomIndex] = temp;
    // 下面逻辑完全不变
    // pivot，i，j的定义在上边已经介绍
    int pivot = data[left], j = left;
    for (int i = left + 1 ; i <= right; i ++) {
        if (data[i] < pivot) {
            j++;
            // swap i and j + 1
            temp = data[j];
            data[j] = data[i];
            data[i] = temp;
        }
    }
    // swap left and j
    data[left] = data[j];
    data[j] = pivot;
    return j;
}

/**
 * 为了方便大家观看，这个插入排序的代码是直接从上一篇中拿过来的
 * 对data[l...r]的区间使用插入排序
 * @param data 待排序数组
 * @param l 起始index，代表left
 * @param r 结尾index，代表right
 */
private static void insertSort(int[] data, int l, int r) {
  for( int i = l + 1 ; i <= r ; i ++ ){
    int e = data[i];
    int j = i;
    for (; j > l && data[j-1] > e; j--) {
      data[j] = data[j - 1];
    }
    data[j] = e;
  }
}

单路快速排序总结

到此为止，我们的快排已经能够完美解决随机数组和几乎有序数组的排序问题。

可以看到，为了避免快排的时间复杂度退化为最坏的时间复杂度 O(n^2)，我们实际上是用随机函数来编写了一个随机化算法（randomized algorithm）。也就是说，我们不能保证我们的算法是一定非常快的，但是可以保证我们的算法在非常非常高的概率下都能非常快。

为什么还有双路、三路快排？

我们的代码完美了吗？当然还不够，因为还是忽略了一种情况：如果当待排序数组有非常多的重复值时，会发生什么事情？

大家仍然可以在自己的 ide 上测试一下，会发现，当随着数据量增大，快排依然会越来越慢，说明此时快排又退化到了最坏时间复杂度 O(n^2)。这又是为什么呢？

当然小标题已经暴露了解决方案，大家可以自己先想想，分析一下。

因为已经写的够长啦，大家可以先消化一下，欲知后事如何且听下回分解…

欢迎关注我的其它发布渠道