Yangsanity's Blog

Life was like a box of chocolates

0%

插入排序

发表于 分类于 阅读次数： Disqus：

不吹不黑，不捧不踩，插入排序（insertion sort）是真的很重要。你不会到现在还以为O(n^2)级别的排序算法都一无是处吧？如果是的话，希望通过本文能够让你对这个观念有个新的认识。

插入排序思想

插入排序的思想其实也很简单，我先从一个简单的例子说起。还记得本文的封面图是什么吗？嗯，扑克牌。大家肯定都玩过扑克牌，我们从牌桌上一张一张拿起扑克牌，然后在手里将扑克牌按照大小顺序插入到合适的位置，其实这整个过程大体上就是插入排序的思想。

再正式点的描述一下插入排序的思想，就是通过构建有序序列，对于未排序的数据，在已排序序列中从后向前扫描，找到相应位置并插入。

使用插入排序为一列数字进行排序的过程（picture from Wikipedia）

接下来就用个简单的demo来演示一下整个过程吧。待排序数组如下：

2 5 4 8 7 3 1 6

比较和交换的详细过程为：
（1）从数组第二个位置向前寻找插入的位置（为什么不从第一个位置开始？因为第一个数字自己本身可以认为就是有序的），5 > 2，保持不变
（2）从数组第三个位置向前寻找插入的位置，4 < 5，交换位置；4 > 2，保持不变

2 4 5 8 7 3 1 6

（3）从数组第四个位置向前寻找插入的位置，8 > 5，保持不变
（4）从数组第五个位置开始向前寻找插入的位置，7 < 8，交换位置；7 > 5，保持不变

2 4 5 7 8 3 1 6
（5）从数组第六个位置向前寻找插入的位置，3 < 8，交换位置；3 < 7，交换位置；3 < 5，交换位置；3 < 4，交换位置；3 > 2，保持不变
2 3 4 5 7 8 1 6
（6）从数组第七个位置向前寻找插入的位置，1 < 8，交换位置；1 < 7，交换位置；1 < 5，交换位置；1 < 4，交换位置；1 < 3，交换位置；1 < 2，交换位置
1 2 3 4 5 7 8 6
（7）从数组第八个位置向前寻找插入的位置，6 < 8，交换位置；6 < 7，交换位置；6 > 5，保持不变
1 2 3 4 5 6 7 8
至此，整个插入排序过程结束。

插入排序代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * insertionSort
 * @param data 待排序数组
 * @return 排序后的数组
 */
private int[] insertionSort(int[] data) {
  // swap 时用到的临时变量
  int temp;
  // 从第 1 个元素开始遍历，因为第 0 个元素自己本身就是有序的
  for (int i = 1; i < data.length; i++) {
    // 从第 j 个位置开始往前遍历，寻找插入位置
    for (int j = i; j > 0 && data[j] < data[j - 1]; j--) {
      // swap
      temp = data[j];
      data[j] = data[j - 1];
      data[j - 1] = temp;
    }
  }
  return data;
}

插入排序优化

比较上面版本的插入排序代码和上一篇介绍的选择排序代码，我们会发现它们两个都是外循环嵌套内循环，而且插入排序在内循环中是会提前结束的，所以按理说插入排序应该更快一些。

其实不然，在某些情况下，上面版本的插入排序是比选择排序慢的。这是为什么呢？大家不要忽略了，虽然插入排序在内循环中会提前结束，但是插入排序还有交换元素的代价，这个操作可比比较元素大小还要耗时。

所以，我们优化插入排序的思路也出来了，我们的目的就是要让插入排序也在内循环中只交换一次。

具体在代码优化实现上，我们需要在内循环中，先把要寻找正确位置的元素记录下来，然后总是将较大的元素向右移动，直到找到正确的位置然后插入该元素即可。具体思路如下图所示：

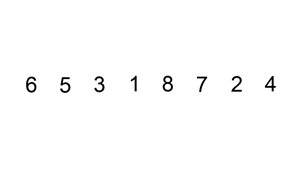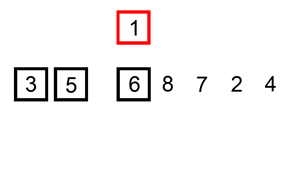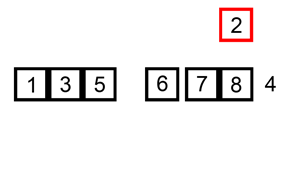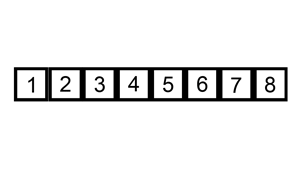
（picture from Wikipedia）

插入排序优化代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * insertionSort
 * @param data 待排序数组
 * @return 排序后的数组
 */
public int[] insertionSort(int[] data) {
  // e 为我们要为其寻找插入位置的元素；j 为元素 e 最终应该插入的位置
  int e, j;
  for (int i = 1; i < data.length; i++) {
    e = data[i];
    // 在寻找 e 插入位置的过程中，较大的元素向右移动
    for (j = i; j > 0 && data[j - 1] > e; j--) {
      data[j] = data[j - 1];
    }
    // 将 e 插入正确的位置
    data[j] = e;
  }
  return data;
}

插入排序再优化

实际上，插入排序还可以再优化。熟悉二分查找的同学肯定就想到了，因为数组前面都是有序区，所以可以在有序区中采用二分查找来减少比较的次数，从而加快速度。

不过，这种算法其实可以认为是插入排序的一个变种，也被称为二分查找插入排序。

插入排序再优化代码

这里直接给出代码，不熟悉二分查找的同学可以预习一下，或者在后面的文章中我会再说说二分查找算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * insertionSort
 * @param data 待排序数组
 * @return 排序后的数组
 */
public int[] insertionSort(int[] data) {
  int e, left, right, mid;
  for (int i = 1; i < data.length; i++) {
    e = data[i];
    left = 0;
    right = i - 1;
    while (left <= right) {
      // 大家可以思考一下这里计算 mid 为什么不用 (left + right) / 2 ？
      // 其实是为了防止溢出，这里也是以前 jdk 底层实现二分查找的一个 bug，读者可以体会一下
      mid = left + ((right - left) >> 1);
      if (data[mid] > e) {
        right = mid - 1;
      } else {
        // 元素相同时，插入在后面的位置
        left = mid + 1;
      }
    }
    // 将插入位置后面的元素都后移一位
    System.arraycopy(data, left, data, left + 1, i - left);
    // 插入元素
    data[left] = e;
  }
  return data;
}

复杂度和稳定性分析

  1. 时间复杂度

  • 最优时间复杂度：O(n)

    • 当用优化后的插入排序代码进行排序时，如果待排序数组本来就是有序的，那么在内循环中，每次比较时都会发现当前元素的位置就是它在数组中的正确位置，直接结束内循环进入下一次循环。假定待排序数组长度为 n，那么最优时间复杂度即为 O(n)。

  • 最坏时间复杂度：O(n^2)

  • 平均时间复杂度：O(n^2)

  1. 空间复杂度：O(1)
  • 整个过程都是原地排序，并没有用到其它辅助的空间。
  1. 插入排序是一种稳定排序。

深入理解插入排序

插入排序 vs 选择排序

插入排序和选择排序都属于O(n^2)级别的排序算法，两者的最大区别是：对于内循环，插入排序可以提前结束，而选择排序必须让内外层循环都完全执行完成。所以选择排序在任何情况下都是非常慢的。如果对选择排序的思想有点模糊的话，可以点击文章的底部链接再复习一下。

插入排序的重要性质

除了可以提前终止内循环外，插入排序还有一个非常重要的性质：在数组近乎有序的情况下，它的性能会非常高，甚至比后面要介绍的O(n * logn)级别的排序算法还要快。

正是因为这个性质，插入排序不仅可以在更加复杂的排序算法中作为一个子过程来优化（在后面说到归并排序和快速排序优化时会用到），而且还具有非常重要的实际意义。

很多时候，在实际应用中，我们处理的真实数据就是近乎有序的。比如日志，按理来说日志都是有序的，但是在生成日志时有可能因为某些错误或程序运行时间过长等原因，导致有几条无序的日志，这时如果使用插入排序来处理，性能会更好。

插入排序的引申

通过插入排序算法还可以引申出另一个重要的排序算法，希尔排序（shell sort），在后面的文章中也会说到。

最后一问，你还认为O(n^2)级别的排序算法都一无是处吗？

欢迎关注我的其它发布渠道